
题目列表(包括答案和解析)
在四棱锥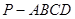 中,
中,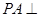 平面
平面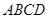 ,底面
,底面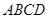 为矩形,
为矩形,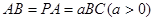 .
.
(Ⅰ)当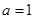 时,求证:
时,求证: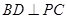 ;
;
(Ⅱ)若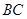 边上有且只有一个点
边上有且只有一个点 ,使得
,使得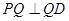 ,求此时二面角
,求此时二面角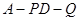 的余弦值.
的余弦值.
【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,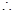
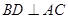
又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使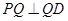 ,只要
,只要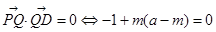
所以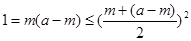 ,即
,即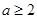 ………6分
………6分
由此可知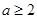 时,存在点Q使得
时,存在点Q使得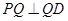
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得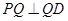
由此知道a=2, 设平面POQ的法向量为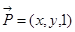
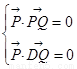 ,所以
,所以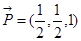 平面PAD的法向量
平面PAD的法向量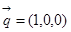
则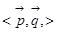 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以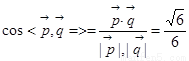
因此二面角A-PD-Q的余弦值为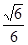
解:(Ⅰ)当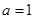 时,底面ABCD为正方形,
时,底面ABCD为正方形,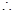
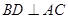
又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使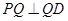 ,只要
,只要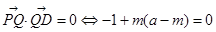
所以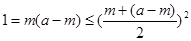 ,即
,即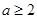 ………6分
………6分
由此可知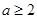 时,存在点Q使得
时,存在点Q使得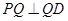
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得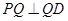 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为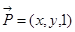
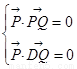 ,所以
,所以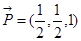 平面PAD的法向量
平面PAD的法向量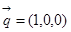
则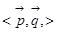 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以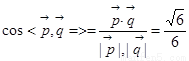
因此二面角A-PD-Q的余弦值为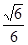
如图,将一张矩形的纸对折以后略微展开,竖立在桌面上,说明折痕为什么与桌面垂直.
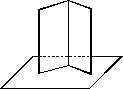
从图中可直观地看出,折痕垂直于对折后的纸与桌面所形成的交线.由直线与平面垂直的判定定理知,折痕与桌面垂直.那么在折痕垂直于纸与桌面的交线未知的情况下,单凭折后的纸与桌面垂直,能否得出折痕与桌面垂直?转化为数学语言,即如果两个相交平面都垂直于第三个平面,那么它们的交线也垂直于第三个平面吗?下面用不同的方法证明.
如图,已知平面α⊥平面β,平面α⊥平面γ,且β∩γ=a,β∩α=l,γ∩α=m.
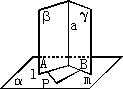
求证:a⊥α.
如图所示的长方体 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形,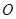 为
为 与
与 的交点,
的交点,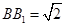 ,
, 是线段
是线段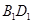 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: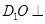 平面
平面 ;
;
(Ⅲ)求二面角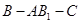 的大小.
的大小.
【解析】本试题主要考查了线面平行的判定定理和线面垂直的判定定理,以及二面角的求解的运用。中利用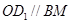 ,又
,又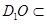 平面
平面 ,
,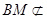 平面
平面 ,∴
,∴ 平面
平面 由
由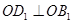 ,
,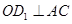 ,又
,又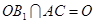 ,∴
,∴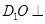 平面
平面 .
可得证明
.
可得证明
(3)因为∴ 为面
为面 的法向量.∵
的法向量.∵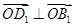 ,
,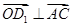 ,
,
∴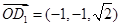 为平面
为平面 的法向量.∴利用法向量的夹角公式,
的法向量.∴利用法向量的夹角公式,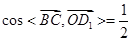 ,
,
∴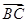 与
与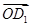 的夹角为
的夹角为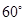 ,即二面角
,即二面角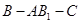 的大小为
的大小为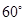 .
.
方法一:解:(Ⅰ)建立如图所示的空间直角坐标系.连接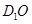 ,则点
,则点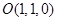 、
、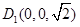 ,
,

∴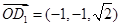 ,又点
,又点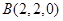 ,
,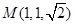 ,∴
,∴
∴ ,且
,且 与
与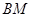 不共线,∴
不共线,∴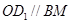 .
.
又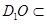 平面
平面 ,
,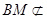 平面
平面 ,∴
,∴ 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵ ,
,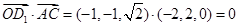
∴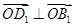 ,
,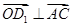 ,即
,即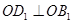 ,
,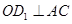 ,
,
又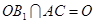 ,∴
,∴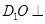 平面
平面 . ………8分
. ………8分
(Ⅲ)∵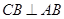 ,
,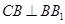 ,∴
,∴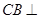 平面
平面 ,
,
∴ 为面
为面 的法向量.∵
的法向量.∵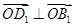 ,
,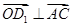 ,
,
∴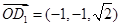 为平面
为平面 的法向量.∴
的法向量.∴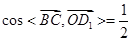 ,
,
∴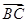 与
与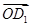 的夹角为
的夹角为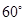 ,即二面角
,即二面角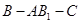 的大小为
的大小为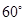
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com