
题目列表(包括答案和解析)
| 2 |
| 2 |
| AM |
| MB |
| 1 |
| 2 |
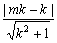
(Ⅰ)若直线AP的斜率为k,且|k|∈[![]() ,
,![]() ],求实数m的取值范围;
],求实数m的取值范围;
(Ⅱ)当m =![]() +1时,△APQ的内心恰好是点M,求此双曲线的方程.
+1时,△APQ的内心恰好是点M,求此双曲线的方程.
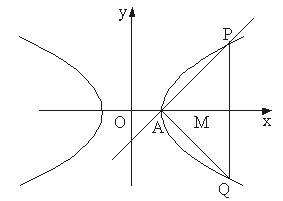
(Ⅰ)若直线AP的斜率为k,且|k|∈[![]() ,
,![]() ],求实数m的取值范围;
],求实数m的取值范围;
(Ⅱ)当m =![]() +1时,△APQ的内心恰好是点M,求此双曲线的方程.
+1时,△APQ的内心恰好是点M,求此双曲线的方程.
(12分)已知双曲线![]() 的渐近线方程是
的渐近线方程是![]() ,且它的一条准线与渐近线
,且它的一条准线与渐近线![]() 及
及![]() 轴
轴
围成的三角形的周长是![]()
(I)求以![]() 的两个顶点为焦点,以
的两个顶点为焦点,以![]() 的焦点为顶点的椭圆
的焦点为顶点的椭圆![]() 的方程;
的方程;
(II)![]() 是椭圆
是椭圆![]() 的长为
的长为![]() 的动弦,
的动弦,![]() 为坐标原来点,求
为坐标原来点,求![]() 的面积
的面积![]() 的取值范围。
的取值范围。
已知双曲线 的一条渐近线方程是
的一条渐近线方程是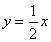 ,它的一个焦点在抛物线
,它的一个焦点在抛物线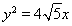 的准线上,点
的准线上,点 是双曲线
是双曲线 右支上相异两点,且满足
右支上相异两点,且满足
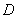 为线段
为线段 的中点,直线
的中点,直线 的斜率为
的斜率为
(1)求双曲线 的方程;
的方程;
(2)用 表示点
表示点 的坐标;
的坐标;
(3)若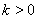 ,
,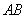 的中垂线交
的中垂线交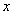 轴于点
轴于点 ,直线
,直线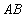 交
交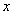 轴于点
轴于点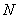 ,求
,求 的面积的取值范围.
的面积的取值范围.
说明:
一、本解答给出一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则。
二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得累加分。
四、只给整数分数,选择题和填空题不给中间分数。
一、选择题:每小题5分,满分60分。
1―5 DBCAB 6―10 ABDAD 11―12CC
二、填空题:每题5分,共20分
13. 14.
14. 15.2000 16.②③
15.2000 16.②③
三、解答题(满分70分)
17.本小题主要考查正弦定理、余弦定理,三角形面积公式等基础知识。
解:(1)
 (5分)
(5分)
(2)将 ,
,

18.本小题主要考查概率的基本知识与分类思想,独立重复试验概率问题,考查运用数学知
识分析问题解决问题的能力。
解:(1)设甲获胜为事件B,则甲获胜包括甲以4:2获胜和甲以4:3获胜两种情况:

 (5分)
(5分)
(2)随机变量ξ可能的取值为4,5,6,7,

ξ的分布列为:
ξ
4
5
6
7
P




 (12分)
(12分)
19.本小题主要考查正四棱柱中线线位置关系、线面垂直判定、三垂线定理、二面角等基础知识,考查空间想象能力、逻辑思维能力、运算能力以及空间向量的应用。
|