
题目列表(包括答案和解析)
(25分)地球赤道表面附近处的重力加速度为![]() ,磁场的磁感应强度的大小
,磁场的磁感应强度的大小![]() ,方向沿经线向北。赤道上空的磁感应强度的大小与
,方向沿经线向北。赤道上空的磁感应强度的大小与![]() 成反比(r为考察点到地心的距离),方向与赤道附近的磁场方向平行。假设在赤道上空离地心的距离
成反比(r为考察点到地心的距离),方向与赤道附近的磁场方向平行。假设在赤道上空离地心的距离![]() (
(![]() 为地球半径)处,存在厚度为10km的由等数量的质子和电子的等离子层(层内磁场可视为匀强磁场),每种粒子的数密度非常低,带电粒子的相互作用可以忽略不计。已知电子的质量
为地球半径)处,存在厚度为10km的由等数量的质子和电子的等离子层(层内磁场可视为匀强磁场),每种粒子的数密度非常低,带电粒子的相互作用可以忽略不计。已知电子的质量![]() ,质子的质量
,质子的质量![]() ,电子电荷量为
,电子电荷量为![]() ,地球的半径
,地球的半径![]() 。
。
1.所考察的等离子层中的电子和质子一方面作无规则运动,另一方面因受地球引力和磁场的共同作用会形成位于赤道平面内的绕地心的环行电流,试求此环行电流的电流密度。
2.现设想等离子层中所有电子和质子,它们初速度的方向都指向地心,电子初速度的大小![]() ,质子初速度的大小
,质子初速度的大小![]() 。试通过计算说明这些电子和质子都不可能到到达地球表面。
。试通过计算说明这些电子和质子都不可能到到达地球表面。
(25分)地球赤道表面附近处的重力加速度为![]() ,磁场的磁感应强度的大小
,磁场的磁感应强度的大小![]() ,方向沿经线向北。赤道上空的磁感应强度的大小与
,方向沿经线向北。赤道上空的磁感应强度的大小与![]() 成反比(r为考察点到地心的距离),方向与赤道附近的磁场方向平行。假设在赤道上空离地心的距离
成反比(r为考察点到地心的距离),方向与赤道附近的磁场方向平行。假设在赤道上空离地心的距离![]() (
(![]() 为地球半径)处,存在厚度为10km的由等数量的质子和电子的等离子层(层内磁场可视为匀强磁场),每种粒子的数密度非常低,带电粒子的相互作用可以忽略不计。已知电子的质量
为地球半径)处,存在厚度为10km的由等数量的质子和电子的等离子层(层内磁场可视为匀强磁场),每种粒子的数密度非常低,带电粒子的相互作用可以忽略不计。已知电子的质量![]() ,质子的质量
,质子的质量![]() ,电子电荷量为
,电子电荷量为![]() ,地球的半径
,地球的半径![]() 。
。
1.所考察的等离子层中的电子和质子一方面作无规则运动,另一方面因受地球引力和磁场的共同作用会形成位于赤道平面内的绕地心的环行电流,试求此环行电流的电流密度。
2.现设想等离子层中所有电子和质子,它们初速度的方向都指向地心,电子初速度的大小![]() ,质子初速度的大小
,质子初速度的大小![]() 。试通过计算说明这些电子和质子都不可能到到达地球表面。
。试通过计算说明这些电子和质子都不可能到到达地球表面。
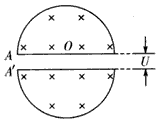
(18分)
1932年美国物理学家劳伦斯发明了回旋加速器,巧妙地利用带电粒子在磁场中的运动特点,解决了粒子的加速问题。现在回旋加速器被广泛应用于科学研究和医学设备中。
某型号的回旋加速器的工作原理如图甲所示,图为俯视图乙。回旋加速器的核心部分为D形盒,D形盒装在真空容器中,整个装置放在巨大的电磁铁两极之间的强大磁场中,磁场可以认为是匀强在场,且与D形盒盒面垂直。两盒间狭缝很小,带电粒子穿过的时间可以忽略不计。D形盒半径为R,磁场的磁感应强度为B。设质子从粒子源A处时入加速电场的初速度不计。质子质量为m、电荷量为+q。加速器接一定涉率高频交流电源,其电压为U。加速过程中不考虑相对论效应和重力作用。
(1)求质子第1次经过狭缝被加速后进入D形盒运动轨道的半径r1;
(2)求质子从静止开始加速到出口处所需的时间t ;
(3)如果使用这台回旋加速器加速α粒子,需要进行怎样的改动?请写出必要的分析及推理。
 |
1932年美国物理学家劳伦斯发明了回旋加速器,巧妙地利用带电粒子在磁场中的运动特点,解决了粒子的加速问题。现在回旋加速器被广泛应用于科学研究和医学设备中。

某型号的回旋加速器的工作原理如图甲所示,图乙为俯视图。回旋加速器的核心部分为D形盒,D形盒装在真空容器里,整个装置放在巨大的电磁铁两极之间的强大磁场中,磁场可以认为是匀强磁场,且与D形盒底面垂直。两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计,D形盒的半径力R,磁场的磁感应强度为B。设质子从粒子源A处进入加速电场的初速度不计。质子质量为m、电荷量为+q。加速器接一定频率高频交变电源,其电压为U。加速过程中不考虑相对论效应和重力作用。
(1)求质子第1次经过狭缝被加速后进人D形盒运动的轨道半径r1;
(2)求质子从静止开始加速到出口处所需的时间t;
(3)如果使用这台回旋加速器加速α粒子,需要进行怎样的改动?请写出必要的分析与推理。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com