
题目列表(包括答案和解析)
解:(1)点C的坐标为![]() .
.
∵ 点A、B的坐标分别为![]() ,
,
∴ 可设过A、B、C三点的抛物线的解析式为![]() .
.
将![]() 代入抛物线的解析式,得
代入抛物线的解析式,得![]() .
.
∴ 过A、B、C三点的抛物线的解析式为![]() .
.
 (2)可得抛物线的对称轴为
(2)可得抛物线的对称轴为![]() ,顶点D的坐标为
,顶点D的坐标为
![]() ,设抛物线的对称轴与x轴的交点为G.
,设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为![]() .
.
设点P的坐标为![]() .
.
解法一:如图8,作OP∥AD交直线BC于点P,
连结AP,作PM⊥x轴于点M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ![]() ,即
,即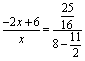 .
.
解得![]() . 经检验
. 经检验![]() 是原方程的解.
是原方程的解.
此时点P的坐标为![]() .
.
但此时![]() ,OM<GA.
,OM<GA.
∵ ![]()
∴ OP<AD,即四边形的对边OP与AD平行但不相等,
∴ 直线BC上不存在符合条件的点P. - - - - - - - - - - - - - - - - - - - - - 6分
解法二:如图9,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于
点N. 则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由![]() ,可得E点的坐标为
,可得E点的坐标为![]() .
.
NE=EG=![]() , ON=OE-NE=
, ON=OE-NE=![]() ,NP=DG=
,NP=DG=![]() .
.
∴ 点P的坐标为![]() .∵ x=
.∵ x=![]() 时,
时,![]() ,
,
∴ 点P不在直线BC上.
∴ 直线BC上不存在符合条件的点P .

(3)![]() 的取值范围是
的取值范围是![]() .
.
 (2012•柳州)如图,在△ABC中,AB=2,AC=BC=
(2012•柳州)如图,在△ABC中,AB=2,AC=BC=| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| x2-2 |
| x2-2 |
| x2-x1 |
| 2 |
| x1+x2 |
| 2 |
| y2-y1 |
| 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

如图,在△ABC中,AB=2,AC="BC=" 5 .
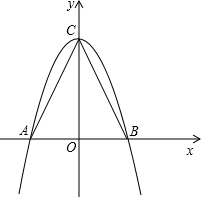
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD= S△ABC;
S△ABC;
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4-4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2-4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=-1.
当x2=3,即y2=3,∴y3=" 3" ,y4="-" 3 .
所以,原方程的解是y1=1,y2=-1,y3=" 3" ,y4="-" 3 .
再如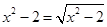 ,可设
,可设 ,用同样的方法也可求解.
,用同样的方法也可求解.
如图,在直角坐标系中,![]() 是原点,
是原点,![]() 三点的坐标分别
三点的坐标分别![]() ,四边形
,四边形![]() 是梯形,点
是梯形,点![]() 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点![]() 沿
沿![]() 向终点
向终点![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位,点
个单位,点![]() 沿
沿![]() 向终点
向终点![]() 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
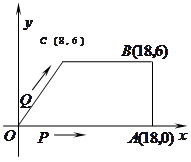
(1)求直线![]() 的解析式.
的解析式.
(2)设从出发起,运动了![]() 秒.如果点
秒.如果点![]() 的速度为每秒
的速度为每秒![]() 个单位,试写出点
个单位,试写出点![]() 的坐标,并写出此时
的坐标,并写出此时![]() 的取值范围.
的取值范围.
(3)设从出发起,运动了![]() 秒.当
秒.当![]() ,
,![]() 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形![]() 的周长的一半,这时,直线
的周长的一半,这时,直线![]() 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出![]() 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
【解析】(1)根据待定系数法就可以求出直线OC的解析式(2)本题应分Q在OC上,和在CB上两种情况进行讨论.即0≤t≤5和5<t≤10两种情况(3)P、Q两点运动的路程之和可以用t表示出来,梯形OABC的周长就可以求得.当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,就可以得到一个关于t的方程,可以解出t的值.梯形OABC的面积可以求出,梯形OCQP的面积可以用t表示出来.把t代入可以进行检验
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com