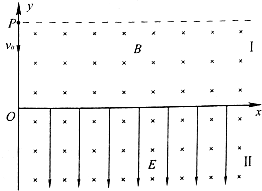（2010?南京二模）如图所示，在y≤5

3

×10-2m的空间有垂直纸面向里的匀强磁场，磁感应强度B=4×10^-3T，在y≤0空间同时存在沿y轴负方向的匀强电场，电场强度E=40

3

V/m．一个质量m=6.4×10^-27kg、带电量g=十3.2×10^-19C的带电粒子以初速度v．=2×10⁴m/s从y轴上的P点（纵坐标为5

3

×10-2m）出发，沿着一y方向进入区域I．粒子重力不计，粒子在整个运动过程中始终没有穿出电磁场区域．
（1）求带电粒子第一次穿越X轴时的横坐标x；
（2）请结合运动合成和分解的知识，求出带电粒子在区域Ⅱ中到达最低点的纵坐标y
（3）求带电粒子从进入区域I开始到第二次穿越x轴时经过的时间t．

查看答案和解析>>

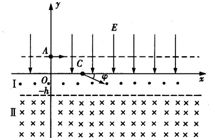
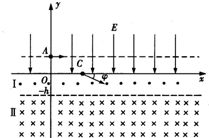如图所示，平面直角坐标系xOy中，在y＞0的区域存在沿y轴负方向的匀强电场，场强大小为E．在-h＜y＜0的区域I中存在垂直纸面向外的匀强磁场，磁感应强度大小为B．在y＜-h的区域Ⅱ中存在垂直纸面向里的匀强磁场，磁感应强度大小为2B．且是y轴上的一点，C是x轴上的一点．一质量为m、电荷量为q的带正电的粒子以某一初速度．沿x轴正方向从A点进入电场区域，继而通过C点以速度方向与x轴夹角为φ=30°进入磁场区域I，并以垂直边界y=-h的速度进入磁场区域Ⅱ，粒子重力不计．试求：
（1）粒子经过C点时的速度大小a；
（2）A、C两点与O点间的距离y₀、x₀；
（3）粒子从A点出发，经过多长时间可回到y=y₀处？

查看答案和解析>>

查看答案和解析>>

如图所示，在的空间有垂直纸面向里的匀强磁场，磁感应强度B=4×10^-3T，在y≤0空间同时存在沿y轴负方向的匀强电场，电场强度一个质量m=6.4×10^-27kg带电量q=+3.2×10^-19C的带电粒子以初速度v₀=2×l0⁴m/s从y轴上的P点（纵坐标为）出发，沿着-y方向进入区域I。粒子重力不计，粒子在整个运动过程中始终没有穿出电磁场区域。
（1）求带电粒子第一次穿越x轴时的横坐标x；
（2）请结合运动合成和分解的知识，求出带电粒子在区域Ⅱ中到达最低点的纵坐标y。
（3）求带电粒子从进入区域I开始到第二次穿越x轴时经过的时间t。

查看答案和解析>>

如图所示，平面直角坐标系xOy中，在y＞0的区域存在沿y轴负方向的匀强电场，场强大小为E．在-h＜y＜0的区域I中存在垂直纸面向外的匀强磁场，磁感应强度大小为B．在y＜-h的区域Ⅱ中存在垂直纸面向里的匀强磁场，磁感应强度大小为2B．且是y轴上的一点，C是x轴上的一点．一质量为m、电荷量为q的带正电的粒子以某一初速度．沿x轴正方向从A点进入电场区域，继而通过C点以速度方向与x轴夹角为φ=30°进入磁场区域I，并以垂直边界y=-h的速度进入磁场区域Ⅱ，粒子重力不计．试求：
（1）粒子经过C点时的速度大小a；
（2）A、C两点与O点间的距离y₀、x₀；
（3）粒子从A点出发，经过多长时间可回到y=y₀处？

查看答案和解析>>

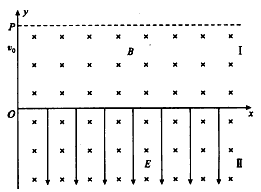
二、选择题：(共48分)

14、B  15、C  16、BD  17、C  18、AD  19、C  20、C  21、BCD

22、实验题：（共18分）

（1）AC (6分)    （2）1B （2分）  E （2分）   G （2分）

 2电路图和实物图各3分，见错无分。

23．物块刚放上传送带时，由牛顿第二定律：

μmg＝ma……………………………………1 2’

得：a＝4m/s²…………………………………2

物块历时t₁后与传送带共速，则：

at₁＝v₀＋a₀t₁…………………………………3 2’

得：t₁＝1s……………………………………4 1’

此过程中物块的位移为：

s₁＝at₁²/2……………………………………5  2’

得：s₁＝2m<s=7m…………………………6 2’

故物体此时尚未到达B点，且此后的过程中由于a₀<μg，物块将和传送带以共同的加速度运动，设又历时t₂到达B点，则：          2’

s－s₁＝at₁t₂＋a₀t₂²/2…………………………7 2’

得：t₂＝1s……………………………………8 1’

物体从A到B历时：t＝t₁＋t₂＝2s…………9 2’

   （其它解法酌情给分）

24、（1）小球运动至第一次碰前：

mgh＝mv₀²/2……………………………………………1  2’

碰撞过程，动量守恒：

mv₀＝（M＋m）v₁…………………………………………2  2’

碰后压缩弹簧过程中，M、m及弹簧系统机械能守恒：

E_pm＝（M＋m）v₁²/2……………………………………3  2’

由1、2、3联立解得：

E_pm＝…………………………………………4  2’

（2）第一次碰后小球向BC轨道运动的初速度即为v₁，由机械能守恒得：

     …………………………………………5  2’

     由1、2、5联立解得：…………6  2’

（3）小球在BC段运动可等效为单摆，其周期为：

T＝………………………………………………7  2’

分析得小球第三次通过B点历时为：

t＝……………………………………………8  2’

由78联立解得：t＝…………………9  2’

 25、（1）粒子在磁场中运动时，由洛仑兹力提供向心力

Bqv₀＝mv₀²/R…………………………………………2’   

得：R＝1m

过M点做初速度v₀的垂线交y轴正方向于P点，则PM＝l/cos45⁰

得：PM＝2m＝2R……………………………………1’

由几何关系得PM为轨迹圆直径，P点即为粒子穿过y轴正半轴的位置

OP＝PM sin45⁰＝m……………………………2’

由圆的对称性得此处速度与y轴夹角为θ＝45⁰………………2’

  （2）设粒子由P点到N点历时t₁，则：

x方向：v₀sin45⁰－Eqt₁/m＝0……………………………………2’

y方向：v₀t₁cos45⁰＝OP…………………………………………2’

联立求解，代入数据得：t1＝0.1s  E＝2V/m≈2.82 V/m…2’

  （3）粒子能到达O点…………………………………………………1’

粒子在磁场中的运动周期为：T＝2πm/Bq……………………2’

从M点运动到O点经过的轨迹如图：（略）

经历的时间为：t＝T/2+3T/4+2t₁………………………………2’

代入数据得：t＝(π/8+0.2)s≈0.59s……………………………2’