
题目列表(包括答案和解析)
已知椭圆 的方程为
的方程为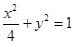 ,双曲线
,双曲线 的左、右焦点分别为
的左、右焦点分别为 的左、右顶点,而
的左、右顶点,而 的左、右顶点分别是
的左、右顶点分别是 的左、右焦点,
的左、右焦点,
(1)求双曲线 的方程;
的方程;
(2)若直线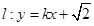 与椭圆
与椭圆 及双曲线
及双曲线 都恒有两个不同的交点,且
都恒有两个不同的交点,且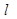 与
与 的两个交点A和B满足
的两个交点A和B满足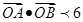 (其中0为原点),求k的取值范围。
(其中0为原点),求k的取值范围。
已知椭圆 的方程为
的方程为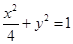 ,双曲线
,双曲线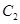 的左、右焦点分别为
的左、右焦点分别为 的左、右顶点,而
的左、右顶点,而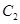 的左、右顶点分别是
的左、右顶点分别是 的左、右焦点。
的左、右焦点。
(1)求双曲线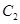 的方程;
的方程;
(2)若直线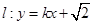 与椭圆
与椭圆 及双曲线
及双曲线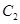 都恒有两个不同的交点,且L与的两个焦点A和B满足
都恒有两个不同的交点,且L与的两个焦点A和B满足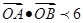 (其中O为原点),求
(其中O为原点),求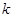 的取值范围。
的取值范围。
已知椭圆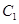 的方程为
的方程为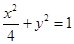 ,双曲线
,双曲线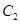 的左、右焦点分别为
的左、右焦点分别为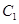 的左、右顶点,而
的左、右顶点,而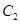 的左、右顶点分别是
的左、右顶点分别是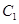 的左、右焦点,
的左、右焦点,
(1)求双曲线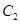 的方程;
的方程;
(2)若直线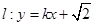 与椭圆
与椭圆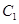 及双曲线
及双曲线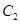 都恒有两个不同的交点,且
都恒有两个不同的交点,且 与
与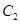 的两个交点A和B满足
的两个交点A和B满足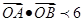 (其中0为原点),求k的取值范围。
(其中0为原点),求k的取值范围。
已知椭圆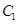 的方程为
的方程为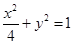 ,双曲线
,双曲线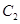 的左、右焦点分别为
的左、右焦点分别为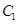 的左、右顶点,而
的左、右顶点,而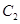 的左、右顶点分别是
的左、右顶点分别是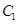 的左、右焦点。
的左、右焦点。
(1)求双曲线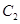 的方程;
的方程;
(2)若直线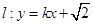 与椭圆
与椭圆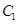 及双曲线
及双曲线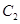 都恒有两个不同的交点,且L与的两个焦点A和B满足
都恒有两个不同的交点,且L与的两个焦点A和B满足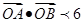 (其中O为原点),求
(其中O为原点),求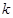 的取值范围。
的取值范围。
 的方程为
的方程为 ,双曲线
,双曲线 的左、右焦点分别为
的左、右焦点分别为 的左、右顶点,而
的左、右顶点,而 的左、右顶点分别是
的左、右顶点分别是 的左、右焦点。
的左、右焦点。 的方程;
的方程; 与椭圆
与椭圆 及双曲线
及双曲线 都恒有两个不同的交点,且L与的两个焦点A和B满足
都恒有两个不同的交点,且L与的两个焦点A和B满足 (其中O为原点),求
(其中O为原点),求 的取值范围。
的取值范围。一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
B
D
D
C
A
A
B
A
C
D
二、填空题13. ; 14.
; 14. ; 15.
; 15. ; 16.
; 16. .
.
三、解答题
17.(1)


 两两相互垂直, 连结
两两相互垂直, 连结 并延长交
并延长交 于F.
于F.


同理可得



 ------------ (6分)
------------ (6分)
(2) 是
是 的重心, F是SB的中点
的重心, F是SB的中点


梯形的高
 --- (12分)
--- (12分)
【注】可以用空间向量的方法
18.解:
(1)设通过3次检测,就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的事件为A
 1分
1分
P(A)=
 5分
5分
所以通过3次检测,就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的概率为
 …6分
…6分
(2)设最多通过4次检测,就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的事件为B … 7分
P(B)=
 11分
11分
所以最多通过4次检测,就可以把3箱含“三聚氰胺”的牛奶全部筛选出来的概率为
 … 12分
… 12分
19.(1) .
.
又
 .
.

 .………6分
.………6分
(2)


又 ,
,
 .从而
.从而

当 且同向时,
且同向时, .………12分
.………12分
20.解:(1)  ,
,
令 ,由
,由 得
得 或
或 .
. .
.
 .
.
当 时,
时, ,当
,当 时,
时, ,所以
,所以 处取极小值,即
处取极小值,即 …………4分
…………4分
(2)

 处取得极小值,即
处取得极小值,即 由
由 即
即





由四边形ABCD是梯形及BC与AD不平行,得 .有
.有 即
即
由四边形ABCD的面积为1,得 即
即 得
得 ,从而
,从而 得
得 ……12分
……12分
21.(1)设双曲线C2的方程为 = 1,则a2 = 4 ? 1 = 3,再由a2 + b2
= c2得b2 = 1.故C2的方程为
= 1,则a2 = 4 ? 1 = 3,再由a2 + b2
= c2得b2 = 1.故C2的方程为 = 1. (5分)
= 1. (5分)
(2)将y = kx + 代入
代入 得(1 + 4k2)x2 + 8
得(1 + 4k2)x2 + 8 kx + 4 = 0,由直线l与椭圆C1恒有两个不同的交点得
kx + 4 = 0,由直线l与椭圆C1恒有两个不同的交点得 (8
(8 )2k2 ? 16 (1 +
4k2) = 16(4k2 ? 1)>0,即k2>
)2k2 ? 16 (1 +
4k2) = 16(4k2 ? 1)>0,即k2> .①(7分)
.①(7分)
将y = kx +  代入
代入 得(1 ? 3k2)x2 ? 6
得(1 ? 3k2)x2 ? 6 kx ? 9 = 0.由直线l与双曲线C2恒有两个不同的交点A、B得
kx ? 9 = 0.由直线l与双曲线C2恒有两个不同的交点A、B得 .即k≠
.即k≠ 且k2<1.②(9分)
且k2<1.②(9分)
设A (xA,yA),B (xB,yB),则xA + xB
=  ,xA,xB =
,xA,xB =  ,由
,由 得xA xB +
yA yB<6,而xA xB +
yA yB = xA xB + (kxA +
得xA xB +
yA yB<6,而xA xB +
yA yB = xA xB + (kxA +  ) (kxb +
) (kxb +  )= (k2 + 1) xA xB +
)= (k2 + 1) xA xB +  k (xA + xB) + 2 = (k2 + 1)?
k (xA + xB) + 2 = (k2 + 1)? ,于是
,于是 <6,即将
<6,即将 .解此不等式得
.解此不等式得 或
或 .
③ (11分)
.
③ (11分)
由①、②、③得 ,
,
故k的取值范围为
 . (12分)
. (12分)
22.(1) .
.
(2)
 ,
,
则 ,
,
 .
.
(3)
 ,
,
即 ①
①
又由于 ,
,
则 ,
,
两式相减得 ,
,
 ,
, 当
当 且
且 时是增函数,
时是增函数,
 的最小值是
的最小值是 , ②
, ②
由①②得:  成立.
成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com