
题目列表(包括答案和解析)
 ,
, (
( )
) 时,函数
时,函数 在其定义域是增函数,求b的取值范围。
在其定义域是增函数,求b的取值范围。 ,
, ,求函数
,求函数 的最小值
的最小值
函数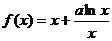 ,其中
,其中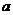 为常数.
为常数.
(1)证明:对任意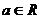 ,
,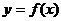 的图象恒过定点;
的图象恒过定点;
(2)当 时,判断函数
时,判断函数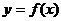 是否存在极值?若存在,求出极值;若不存在,说明理由;
是否存在极值?若存在,求出极值;若不存在,说明理由;
(3)若对任意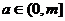 时,
时,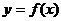 恒为定义域上的增函数,求
恒为定义域上的增函数,求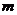 的最大值.
的最大值.
函数![]() ,其中a为常数.
,其中a为常数.
(1)证明:对任意a∈R,y=f(x)的图象恒过定点;
(2)当a=-1时,判断函数y=f(x)是否存在极值?若存在,求出极值;若不存在,说明理由;
(3)若对任意a∈(0,m]时,y=f(x)恒为定义域上的增函数,求m的最大值.
已知![]()
(1)若![]() ,函数
,函数![]() 在其定义域内是增函数,求
在其定义域内是增函数,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,证明:函数
时,证明:函数![]() 只有一个零点;
只有一个零点;
(3)若![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两
两![]() 点,AB
点,AB![]() 中点为
中点为![]() ,求证:
,求证:![]()
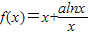 ,其中a为常数.
,其中a为常数.一、选择题

二、填空题
13. ; 14.112; 15.
; 14.112; 15. ; 16.
; 16.
三、解答题
17.解:∵向量 的夹角
的夹角 ,
,

①当 时,
时, ;②当
;②当 时,
时, ;③当
;③当 时,
时,

综上所述:当 时,
时,  的范围是
的范围是 当
当 时,
时, 的范围是
的范围是 ;
;
当 时,
时,  的范围是
的范围是
18.解:(1) ∵ 底面ABC,∴
底面ABC,∴ .又∵
.又∵ 是正三角形,且E为AC的中点,
是正三角形,且E为AC的中点, .又
.又 ,
, 平面PAC.
平面PAC. 平面PEF,
平面PEF,
∴平面 平面PAC.
平面PAC.
(2)取CD的中点F,则点F即为所求.∵E、F分别为CA、CD的中点, .
.
又 平面PEF,
平面PEF, 平面PEF,∴
平面PEF,∴ 平面PEF.
平面PEF.
(3) .
.
19.解:(1)

依题意
 ,
,




(2)
又
在Rt△ABC中,

又
20.解:(I) ,
,
由 ,
,  ,
,
 ,
,
 ,
, ,∴
,∴ 。
。
(II)由 得:
得:
 ,
,
 ,
, ,
,
由②-①得:

 。
。
21解:当年生产x(万件)时,
年生产成本=固定费用+年生产费用 ,
,
年销售收入 ,∵利润=销售收入―生产成本―促销费,
,∵利润=销售收入―生产成本―促销费,
∴

 (万元).
(万元).
当切仅当 即
即 时,
时,
∴该企业2008年的促销费投入7万元时,企业的年利润 (万元)最大.
(万元)最大.
22.解:(1)依题意: ∵
∵ 上是增函数,
上是增函数,
∴ 恒成立,
恒成立,
∴ ∵
∵ ∴b的取值范围为
∴b的取值范围为
(2)设 则函数化为
则函数化为 ,
,
∵ ∴当
∴当 上为增函数,
上为增函数,
当 时,
时, 当
当
 当
当 上为减函数,
上为减函数,
当 时,
时, 综上所述,当
综上所述,当
当 时,
时, ;
;
(3)设点P、Q的坐标是
则点M、N的横坐标为 C1在M处的切线斜率为
C1在M处的切线斜率为
C2在点N处的切线斜率
假设C1在点M处的切线与C2在点N处的切线平行,则
即 则
则




 。设
。设 。
。
令 则
则
∵ ∴
∴ 所以
所以 上单调递增,故
上单调递增,故 ,则
,则 这与①矛盾,假设不成立,故C1在点M处的切线与C2在点N处的切线不平行。
这与①矛盾,假设不成立,故C1在点M处的切线与C2在点N处的切线不平行。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com