练习册

  • 练习册
  • 试题
    (一).三角形中的各种关系 设△ABC的三边为a.b.c.对应的三个角为A.B.C． 1．角与角关系:A+B+C = π. 2．边与边关系:a + b > c.b + c > a.c + a > b. a-b < c.b-c < a.c-a > b． 3．边与角关系: 1)正弦定理 2)余弦定理 c2 = a2+b2-2bccosC.b2 = a2+c2-2accosB.a2 = b2+c2-2bccosA． 它们的变形形式有:a = 2R sinA..． 3)射影定理: a＝b·cosC+c·cosB. b＝a·cosC+c·cosA. c＝a·cosB+c·cosA． 4)正切定理: -----. 5)模尔外得公式: 6)半角定理: 7)面积公式: 【查看更多】

     

    题目列表(包括答案和解析)

    在古希腊，毕达哥拉斯学派把1，3，6，10，15，21，28，…，这些数叫做三角形数，其通项为
    n(n+1)
    2
    ，前n项和为sn=
    n(n+1)(n+2)
    6
    ，如下图所示，有一列三角形数表，其位于三角形的三边及平行于某边的任一直线上的数（当数的个数不少于3时）都分别依次成等差数列，依次记各三角形数表中的所有数之和为an，则a1=
    0+2+6
    4
    =
    2(1+3)
    4
    =2，a2=
    0+3+9+18
    9
    =
    3(1+3+6)
    9
    =
    10
    3
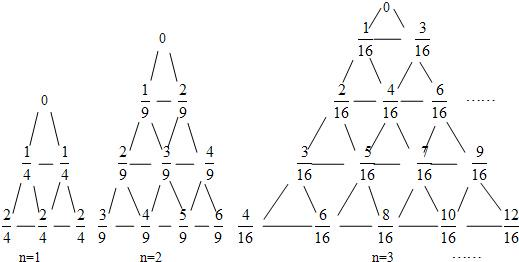
    ．精英家教网
    （1）求a3，a4，并写出an的表达式；
    （2）令bn=
    an
    an+1
    +
    an+1
    an
    ，证明2n＜b1+b2+b3+…+bn＜2n+2（n∈N*）．

    查看答案和解析>>

    以下命题正确的是（　　）
    （1）过一点一定存在和两条异面直线都平行的平面；
    （2）两条平行线中的一条直线与一个平面平行，则另一条也必与这个平面平行；
    （3）各面都是三角形的多面体是三棱锥；
    （4）一条直线平行于一个平面，则夹在它们之间的平行线段长相等．
    A、（1）（2）（3）（4）B、（2）（3）（4）C、（3）（4）D、（4）

    查看答案和解析>>

    精英家教网把自然数按上小下大、左小右大的原则排成如图的三角形数表（每行比上一行多一个数）．设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数的第j个数（如a42=8）．
    （1）试用i表示aii（不要求证明）；
    （2）若aij=2008，求i，j的值；
    （3）记三角形数表从上往下数第n行的各数之和为bn，令cn=
    1，(n=1)
    n
    bn-n
    ，(n≥2)
    ，若数列{cn}的前n项和为Tn，求Tn．

    查看答案和解析>>

    一个盒子中装有形状大小相同的5张卡片,上面分别标有数字1,2,3,4,5,甲乙两人分别从盒子中随机不放回的各抽取一张．

    (Ⅰ)写出所有可能的结果,并求出甲乙所抽卡片上的数字之和为偶数的概率；

    (Ⅱ)以盒子中剩下的三张卡片上的数字作为边长来构造三角形,求出能构成三角形的概率．

     

    查看答案和解析>>

    正 2006 边形 P 的一条对角线称为好的，如果它的两端点将 P 的边界分成的两部分各含P 的奇数条边．P 的边也是好的．

    设 P 被不在 P 的内部相交的 2003 条对角线剖分为三角形．试求这种剖分图中有两条边为好的等腰三角形个数的最大值．

    查看答案和解析>>


    同步练习册答案