某农产品去年各季度的市场价格如下表：

今年某公司计划按去年各季度市场价格的“平衡价m”(平衡价m是这样的一个量：与上年各季度售价差比较，m与各季度售价差的平方和最小)收购该种农产品，并按每100元纳税10元(又称征税率为10个百分点)，计划可收购a万吨，政府为了鼓励收购公司多收购这种农产品，决定将税率降低x个百分点，预测收购量可增加2x个百分点．

(Ⅰ)根据题中条件填空，m＝________(元／吨)；

(Ⅱ)写出税收y(万元)与x的函数关系式；

(Ⅲ)若要使此项税收在税率调节后不少于原计划税收的83.2％，试确定x的取值范围．

某生产流水线，由于改进了设备，预计第一年产量的增长率为160％，以后每年的增长率是前一年的一半．设原来的产量是a．

(Ⅰ)写出改进设备后的第一年，第二年，第三年的产量，并写出第n年与第n－1年(n≥2，n∈N)的产量之间的关系式；

(Ⅱ)由于设备不断老化，估计每年将损失年产量的5％，如此下去，以后每年的产量是否始终是逐年提高？若是，请给予证明；若不是；请说明从第几年起，产量将比上一年减少？

若方程x²＋(m－2)x－m＋5＝0的两个根都大于2，求实数m的取值范围．

阅读下面的解法，回答提出的问题．

解：第一步，令判别式Δ＝(m－2)²－4(－m＋5)≥0，

解得m≥4或m≤－4；

第二步，设两根为x₁，x₂，由x₁＞2，x₂＞2得

，所以．

所以m＜－2．

第三步，由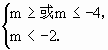得m≤－4．

第四步，由第三步得出结论．

当m∈(－∞，－4]时，此方程两根均大于2．

但当取m＝－6检验知，方程x²－8x＋11＝0两根为x＝4±，其中4－＜2．

试问：产生错误的原因是什么？

某厂在一个空间容积为2000m³的密封车间内生产某种化学药品．开始生产后，每满60分钟会一次性释放出有害气体am³，并迅速扩散到空气中．每次释放有害气体后，车间内的净化设备随即自动工作20分钟，将有害气体的含量降至该车间内原有有害气体含量的r％，然后停止工作，待下一次有害气体释放后再继续工作．安全生产条例规定：只有当车间内的有害气体总量不超过1.25am³时才能正常进行生产．

(Ⅰ)当r＝20时，该车间能否连续正常生产6.5小时？请说明理由；

(Ⅱ)能否找到一个大于20的数据r，使该车间能连续正常生产6.5小时？请说明理由；

(Ⅲ)(本小题为附加题，如果解答正确，加4分，但全卷总分不超过150分)

已知该净化设备的工作方式是：在向外释放出室内混合气体(空气和有害气体)的同时向室内放入等体积的新鲜空气．已知该净化设备的换气量是200m³／分，试证明该设备连续工作20分钟能够将有害气体含量降至原有有害气体含量的20％以下．(提示：我们可以将净化过程划分成n次，且n趋向于无穷大．)

已知M＝(1＋cos2x，1)，N＝(1，sin2x＋a)，(x∈R，a∈R，a是常数)，且y＝(O为坐标原点)

(1)求y关于x的函数关系式y＝f(x)；

(2)若x∈[0，]时，f(x)的最大值为4，求a的值，并说明此时f(x)的图像可由y＝2sin(x＋)的图像经过怎样的变换而得到．