
题目列表(包括答案和解析)
(I)设![]() 是各项均不为零的等差数列
是各项均不为零的等差数列![]() ,且公差
,且公差![]() ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
①当![]() 时,求
时,求![]() 的数值;②求
的数值;②求![]() 的所有可能值;
的所有可能值;
(II)求证:对于一个给定的正整数![]() ,存在一个各项及公差都不为零的等差数列
,存在一个各项及公差都不为零的等差数列![]() ,其中任意三项(按原来的顺序)都不能组成等比数列。
,其中任意三项(按原来的顺序)都不能组成等比数列。
(文)
设函数![]() ,其图象在点
,其图象在点![]() ,
,![]() 处的切线的斜率分别为
处的切线的斜率分别为![]()
(I)求证:![]() ;
;
(II)若函数![]() 的递增区间为
的递增区间为![]() ,求|
,求|![]() |的取值范围;
|的取值范围;
(III)若当![]() 时(
时(![]() 是与
是与![]() 无关的常数),恒有
无关的常数),恒有![]() ,试求
,试求![]() 的最小值。
的最小值。
(I)设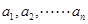 是各项均不为零的等差数列
是各项均不为零的等差数列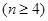 ,且公差
,且公差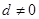 ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
①当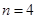 时,求
时,求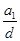 的数值;②求
的数值;②求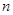 的所有可能值;
的所有可能值;
(II)求证:对于一个给定的正整数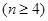 ,存在一个各项及公差都不为零的等差数列
,存在一个各项及公差都不为零的等差数列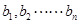 ,其中任意三项(按原来的顺序)都不能组成等比数列。
,其中任意三项(按原来的顺序)都不能组成等比数列。
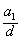 的数值;
的数值;(本小题满分13分)
品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
现设 ,分别以
,分别以 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
 ,
,
则 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。
(Ⅰ)写出 的可能值集合;
的可能值集合;
(Ⅱ)假设 等可能地为1,2,3,4的各种排列,求
等可能地为1,2,3,4的各种排列,求 的分布列;
的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有 ,
,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。
一、选择题(本大题共10小题,每小题5分,共50分)
1―5 ABCDC 6―10 CDBAB
二、填空题(本大题共7小题,每小题4分,共28分)
11. 12.
12. 13.10 14.
13.10 14. 15.1 16.50 17.―1
15.1 16.50 17.―1
三、解答题(本大题共5小题,共72分。解答应写出文字说明、证明过程或演算过程)
18.(本小题满分14分)
解:(I) ………………3分
………………3分
 ………………5分
………………5分
 ………………8分
………………8分
(II)由(I)可得 …………14分
…………14分
19.(本小题满分14分)
解:(I)由 从而
从而

(II) ,
,
 ………………11分
………………11分
若 ………………14分
………………14分
20.(本小题满分14分)
解:(1)在D1B1上取点M,使D1M=1,
连接MB,MF。 ………………1分
∵D1F=1,D1M=1,
|