
题目列表(包括答案和解析)
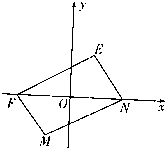 (2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4
(2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4| 2 |
| GO |
| AB |
| 3 |
| 15 |
| 1 |
| 4 |
| PE |
| QE |
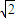 的平行四边形MNEF.平面上的动点G满足|
的平行四边形MNEF.平面上的动点G满足|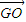 |=2(O为坐标原点)
|=2(O为坐标原点)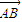 |∈(
|∈(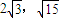 ),求△NPQ内切圆的半径的取值范围.
),求△NPQ内切圆的半径的取值范围.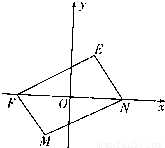
 的平行四边形MNEF.平面上的动点G满足|
的平行四边形MNEF.平面上的动点G满足| |=2(O为坐标原点)
|=2(O为坐标原点) |∈(
|∈( ),求△NPQ内切圆的半径的取值范围.
),求△NPQ内切圆的半径的取值范围.
 )为中点,求直线MN的方程;
)为中点,求直线MN的方程; 恒为定值λ?若存在,求出点E的坐标及实数λ的值;若不存在,请说明理由.
恒为定值λ?若存在,求出点E的坐标及实数λ的值;若不存在,请说明理由.
一、选择题(本大题共10小题,每小题5分,共50分)
1―5 ABCDC 6―10 CDBAB
二、填空题(本大题共7小题,每小题4分,共28分)
11. 12.
12. 13.10 14.
13.10 14. 15.1 16.50 17.―1
15.1 16.50 17.―1
三、解答题(本大题共5小题,共72分。解答应写出文字说明、证明过程或演算过程)
18.(本小题满分14分)
解:(I) ………………3分
………………3分
 ………………5分
………………5分
 ………………8分
………………8分
(II)由(I)可得 …………14分
…………14分
19.(本小题满分14分)
解:(I)由 从而
从而

(II) ,
,
 ………………11分
………………11分
若 ………………14分
………………14分
20.(本小题满分14分)
解:(1)在D1B1上取点M,使D1M=1,
连接MB,MF。 ………………1分
∵D1F=1,D1M=1,
|