
题目列表(包括答案和解析)
设函数f(x)的定义域为R,若存在常数M>0,使得|f(x)|≤M|x|对一切实数x均成立,则称f(x)为F函数,给出下列函数:
①f(x)=0;
②f(x)=x2;
③f(x)=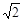 (sinx+cosx);
④f(x)=
(sinx+cosx);
④f(x)=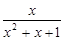 ;
;
⑤f(x)是定义在R上的奇函数,且对于任意实数x1,x2,均有|f(x1)-f(x2)|≤2|x1-x2|。
则其中是F函数的序号是___________________
设函数f(x)的定义域为R,若存在常数M>0,使得|f(x)|≤M|x|对一切实数x均成立,则称f(x)为F函数,给出下列函数:
①f(x)=0; ②f(x)=x2; ③f(x)= (sinx+cosx); ④f(x)=
(sinx+cosx); ④f(x)= ;
;
⑤f(x)是定义在R上的奇函数,且对于任意实数x1,x2,均有|f(x1)-f(x2)|≤2|x1-x2|。
则其中是F函数的序号是___________________
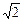 (sinx+cosx); ④f(x)=
(sinx+cosx); ④f(x)=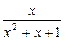 ;
;
| |||||||||||||||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com