
题目列表(包括答案和解析)
已知抛物线![]() ,过M(a,0)且斜率为1的直线
,过M(a,0)且斜率为1的直线![]() 与抛物线交于不同的两点A、B,
与抛物线交于不同的两点A、B,![]() 。
。
(1)求a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值。
分析:这是一道直线与圆锥曲线位置关系的问题,对于(1),可以设法得到关于a的不等式,通过解不等式求出a的范围,即“求范围,找不等式”。或者将a表示为另一个变量的函数,利用求函数的值域求出a的范围。对于(2)首先要把△NAB的面积表示为一个变量的函数,然后再求它的最大值。
投资生产某种产品,并用广告方式促销,已知生产这种产品的年固定投资为10万元,每生产1万件产品还需投入16万元,又知年销量W(万件)与广告费x(万元)之间的函数关系为W=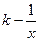 (x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(1)试将年利润y(万元)表示为年广告费x(万元)的函数;
(2)当年广告费为多少万元时,年利润最大?最大年利润是多少万元?
投资生产某种产品,并用广告方式促销,已知生产这种产品的年固定投资为10万元,每生产1万件产品还需投入16万元,又知年销量W(万件)与广告费x(万元)之间的函数关系为W=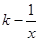 (x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(1)试将年利润y(万元)表示为年广告费x(万元)的函数;
(2)当年广告费为多少万元时,年利润最大?最大年利润是多少万元?
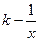 (x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com