
题目列表(包括答案和解析)
ξ | -1 | 0 | 1 |
P |
|
| 8p |
则Eξ等于
A.![]() B.
B.![]() C.-
C.-![]() D.-
D.-![]()
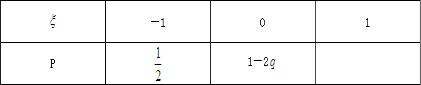
设![]() 是一个离散型随机变量,其分布列如下表,求
是一个离散型随机变量,其分布列如下表,求![]() 的值
的值
|
| -1 | 0 | 1 |
| P |
| 1-2 |
|
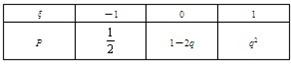
设![]() 是一个离散型随机变量,其分布列如下表,求
是一个离散型随机变量,其分布列如下表,求![]() 值,并求
值,并求![]() .
.
|
| -1 | 0 | 1 |
| P |
|
|
|
分析:根据分布列的两个性质,先确定q的值,当分布列确定时,![]() 只须按定义代公式即可.
只须按定义代公式即可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com