
题目列表(包括答案和解析)
若函数![]() 的一个零点落在区间
的一个零点落在区间![]() 内,则
内,则![]() 的值为
的值为
A.1 B.2 C.3 D.4
若函数![]() 的一个零点落在区间(m,m+1)(m∈N*)内,则m的值为
的一个零点落在区间(m,m+1)(m∈N*)内,则m的值为
1
2
3
4
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
给出下列四个命题, 其中错误的命题有( )个.
(1) 函数 的零点落在区间
的零点落在区间 内;
内;
(2) 函数 上的单调递增区间是
上的单调递增区间是 ;
;
(3) 设 ,且
,且 ,
,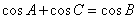 ,则
,则 等于
等于 ;
;
(4) 方程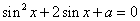 有解,则
有解,则 的取值范围是
的取值范围是 . ( )
. ( )
A.0 B.1 C. 2 D. 3
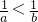
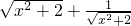 的最小值为2
的最小值为2
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分.
一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分.
1. A 2. D 3. C 4. C 5. B 6. D 7. B 8. A 9. C 10. D 11. B 12. C
二、填空题:本题考查基础知识和基本运算,每小题4分,满分16分.
13.  14.
14.
 15.
15.
 16.
16.

三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17. 本题主要考查三角函数的基本公式,考查运算能力. 满分12分.
解:(Ⅰ)在 中,因为
中,因为 ,
,
所以 .
……………………………(3分)
.
……………………………(3分)
所以
 . …………………………(6分)
. …………………………(6分)
(Ⅱ)根据正弦定理得: ,
,
所以 . ……………………………(9分)
. ……………………………(9分)
所以
 . ………………………………………………………(12分)
. ………………………………………………………(12分)
18.本题主要考查直线与平面的位置关系,考查空间想像能力,推理论证能力和运算求解能
力. 满分12分.
解:(Ⅰ)因为平面ABCD⊥平面ABE,且ABCD是正方形,所以BC⊥平面ABE,
因为G是等边三角形ABE的边AE的中点,所以BG⊥AE,……………(2分)
所以

 .…………………………………………(4分)
.…………………………………………(4分)
(Ⅱ)取DE中点M,连结MG、FM,


 因为MG
因为MG  AD,BF
AD,BF
 AD,所以MG BF,
AD,所以MG BF,
四边形FBGM是平行四边形,所以BG//FM.(6分)
又因为FM 平面EFD,BG
平面EFD,BG 平面EFD,
平面EFD,
所以BG//平面EFD. ………………(8分)
(Ⅲ)因为DA⊥平面ABE,BG 平面ABE,所以DA⊥BG. …………………(9分)
平面ABE,所以DA⊥BG. …………………(9分)
又BG⊥AE,AD AE=A,
AE=A,
所以BG⊥平面DAE,又AP 平面DAE,………………………………(11分)
平面DAE,………………………………(11分)
所以BG⊥AP. ……………………………………………………………(12分)
19. 本题主要考查等差数列、等比数列的基本知识,考查运算求解能力及推理能力. 满分12分.
解:(Ⅰ)设该等差数列的公差为 ,依题意得:
,依题意得: ………(2分)
………(2分)
解得: ………………………………………………………(4分)
………………………………………………………(4分)
所以数列 的通项公式为
的通项公式为 .
………………………………(6分)
.
………………………………(6分)
(Ⅱ)依题意得: ………………(9分)
………………(9分)
 . ………(12分)
. ………(12分)
20. 本题主要考查概率、统计的基本知识,考查应用意识. 满分12分.
解:(Ⅰ)设每个报名者能被聘用的概率为P,依题意有:
 .
.
答:每个报名者能被聘用的概率为0.02. ………………………………………(4分)
(Ⅱ)设24名笔试者中有x名可以进入面试,依样本估计总体可得:
 ,解得:
,解得: ,从表中可知面试的切线分数大约为80分.
,从表中可知面试的切线分数大约为80分.
答:可以预测面试的切线分数大约为80分. ……………………………………(8分)
(Ⅲ)从聘用的四男、二女中选派两人的基本事件有:(a,b),( a,c) , (a, d) ,( a, e) ,
(a, f) ,( b, c) ,(b,d),( b, e) ,( b, f) ,(c, d) ,(c, e),( c, f) ,( d, e) ,( d, f) ,(e, f),共15种.
选派一男一女参加某项培训的种数有:
(a,e) ,( a, f) , (b,e) ,(b, f),(c,e),(c, f) ,(d,e) ,(d, f),共8种
所以选派结果为一男一女的概率为 .
.
答:选派结果为一男一女的概率为 .
…………………………………(12分)
.
…………………………………(12分)
21.本题主要考查圆、直线与椭圆的位置关系等基本知识,考查运算求解能力和分析问题、
解决问题的能力. 满分12分
解:(Ⅰ)由已知得, ,所以
,所以
又 ,所以
,所以 ,椭圆C的方程为
,椭圆C的方程为 ………(3分)
………(3分)
因为 ,所以
,所以 ,可求得
,可求得 或
或 ,…(5分)
,…(5分)
所以 的外接圆D的方程是
的外接圆D的方程是 或
或 .
.
………………………………………………………………(7分)(少一解扣1分)
(Ⅱ)当直线 的斜率不存在时,由(Ⅰ)得
的斜率不存在时,由(Ⅰ)得 ,
, ,
,
可得 ,所以
,所以 .…………………………………(8分)
.…………………………………(8分)
当直线 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为 ,显然
,显然 ,
,
则直线 的方程为
的方程为 ,设点
,设点 ,
,
将 代入方程
代入方程 ,并化简得:
,并化简得:
 ……………………………………(9分)
……………………………………(9分)
可得:
 ,
,
 , ……………………(10分)
, ……………………(10分)
所以
 综上,
综上, .
………………………(12分)
.
………………………(12分)
22.本题主要考查函数的单调性、极值、最值、不等式、方程的解等基本知识,考查运用导
数研究函数性质的方法,考查分类与整合及化归与转化等数学思想. 满分14分.
解:(Ⅰ)依题意,知 的定义域为
的定义域为 .
…………………………………(1分)
.
…………………………………(1分)
当 时,
时, ,
,
 .
………………………………(2分)
.
………………………………(2分)
令 ,解得
,解得 .
.
当 时,
时, ,此时
,此时 单调递增;
单调递增;
当 时,
时, ,此时
,此时 单调递减. ……………………………(3分)
单调递减. ……………………………(3分)
所以 的极大值为
的极大值为 ,此即为最大值 . ……………………(4分)
,此即为最大值 . ……………………(4分)
(Ⅱ) ,
,
所以 ,在
,在 上恒成立,………………(6分)
上恒成立,………………(6分)
所以 ,
, …………………………………(7分)
…………………………………(7分)
当 时,
时, 取得最大值
取得最大值 .所以
.所以 . ………………(9分)
. ………………(9分)
(Ⅲ)因为方程 有唯一实数解,所以
有唯一实数解,所以 有唯一实数解.设
有唯一实数解.设 ,则
,则 .
.
令 ,得
,得 .
.
因为 ,
,
所以 (舍去),
(舍去), , ………(10分)
, ………(10分)
当 时,
时, ,
, 在
在 单调递减,
单调递减,
当 时,
时, ,
, 在
在 单调递增.
单调递增.
当 时,
时, ,
, 取最小值
取最小值 . ……………………(11分)
. ……………………(11分)
因为 有唯一解,所以
有唯一解,所以 .
.
则 ,即
,即
所以 ,
,
因为 ,所以
,所以 . …………………………(12分)
. …………………………(12分)
设函数 ,
,
因为当 时,
时, 是增函数,所以
是增函数,所以 至多有一解.
………(13分)
至多有一解.
………(13分)
因为 ,所以方程
,所以方程 的解为
的解为 ,即
,即 ,
,
解得 ……………………………………………(14分)
……………………………………………(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com