
题目列表(包括答案和解析)
已知不等式![]() 的整数解构成等差数列
的整数解构成等差数列![]() 的前三项,则数列
的前三项,则数列![]() 的第四项为( )
的第四项为( )
A.3 B![]() .-1 C.2 D.3或-1
.-1 C.2 D.3或-1
已知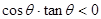 ,那么角
,那么角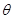 是( )
是( )
A.第一或第二象限角 B. 第二或第三象限角
C. 第三或第四象限角 D. 第一或第四象限角
命题“对顶角相等”的逆命题、否命题、逆否命题中,真命题是( )
(A)上述四个命题 (B)原命题与逆命题
(C)原命题与逆否命题 (D)原命题与否命题
①-2是16的四次方根 ②正数的n次方根有两个 ③a的n次方根就是![]() ④
④![]() =a(a≥0)
=a(a≥0)
A.1
B.2
C.3
D.4
①有些四棱锥有四个顶点 ②存在长方体,使它的两个相对面是正方形 ③有些异面直线没有公垂线
A.0 B.1 C.2 D.3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com