
题目列表(包括答案和解析)
| x2+x+4 | x |
函数 ,其中
,其中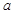 为实常数。
为实常数。
(1)讨论 的单调性;
的单调性;
(2)不等式 在
在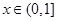 上恒成立,求实数
上恒成立,求实数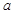 的取值范围;
的取值范围;
(3)若 ,设
,设 ,
,
 。是否存在实常数
。是否存在实常数 ,既使
,既使 又使
又使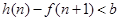 对一切
对一切 恒成立?若存在,试找出
恒成立?若存在,试找出 的一个值,并证明;若不存在,说明理由.
的一个值,并证明;若不存在,说明理由.
 ,其中
,其中 为实常数。
为实常数。 的单调性;
的单调性; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; ,设
,设 ,
,
 。是否存在实常数
。是否存在实常数 ,既使
,既使 又使
又使 对一切
对一切 恒成立?若存在,试找出
恒成立?若存在,试找出 的一个值,并证明;若不存在,说明理由.
的一个值,并证明;若不存在,说明理由.函数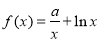 ,其中
,其中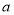 为实常数。
为实常数。
(1)讨论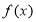 的单调性;
的单调性;
(2)不等式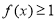 在
在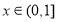 上恒成立,求实数
上恒成立,求实数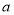 的取值范围;
的取值范围;
(3)若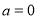 ,设
,设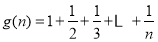 ,
,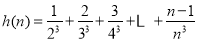
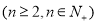 。是否存在实常数
。是否存在实常数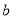 ,既使
,既使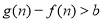 又使
又使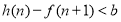 对一切
对一切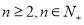 恒成立?若存在,试找出
恒成立?若存在,试找出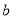 的一个值,并证明;若不存在,说明理由.
的一个值,并证明;若不存在,说明理由.
| x2+x+4 |
| x |
一.DACAC;DBBBC;.files/image131.gif) ;13.
;13. .files/image133.gif) ;14.80;15.-3.
;14.80;15.-3.
16解:(Ⅰ)由图得
X
(0,1)
1
(1,2)
2
0
0
极大值
.files/image146.gif)
极小值
.files/image147.gif)
故当x.files/image149.gif) (0, 1)时,f(x)是增函数,当 x
(0, 1)时,f(x)是增函数,当 x.files/image149.gif) (2,,+∞)时,f(x)也是增函数,
(2,,+∞)时,f(x)也是增函数,
当x.files/image149.gif) (1 ,2)时,f(x)是减函数. ……………………………5分
(1 ,2)时,f(x)是减函数. ……………………………5分
(Ⅱ)依题意得.files/image151.gif) ……………10分 即
……………10分 即.files/image153.gif)
17、解:(Ⅰ)求导得.files/image159.gif) 。……………………………1分
。……………………………1分
即: .files/image165.gif) 1-
1-.files/image167.gif) .…………6分
.…………6分
3
(Ⅱ)由.files/image167.gif) 得:
得:.files/image169.gif) ……7分
……7分
令f′(x)>0,解得 x<-1或x>3;………9分,又令f′(x)< 0,解得 -1<x<3. ……10分
故当x.files/image149.gif) (
(.files/image171.gif) , -1)时,f(x)是增函数,当 x
, -1)时,f(x)是增函数,当 x.files/image149.gif) (3,
(3,.files/image173.gif) )时,f(x)也是增函数,………………12分
)时,f(x)也是增函数,………………12分
当x.files/image149.gif) (-1 ,3)时,f(x)是减函数. ……………………………13分
(-1 ,3)时,f(x)是减函数. ……………………………13分
由题意知,1与3是方程.files/image179.gif) 的两根, …………2分
的两根, …………2分
于是 .files/image181.gif) …………4分
…………4分
.files/image183.gif)
当.files/image185.gif) 时,
时,.files/image187.gif) 当
当.files/image189.gif) 时,
时,.files/image191.gif) 当
当.files/image193.gif) 时,
时,.files/image187.gif)
故当x.files/image149.gif) (
(.files/image171.gif) , 1)时,f(x)是增函数,当 x
, 1)时,f(x)是增函数,当 x.files/image149.gif) (3,
(3,.files/image173.gif) )时,f(x)也是增函数,
)时,f(x)也是增函数,
但当x.files/image149.gif) (1 ,3)时,f(x)是减函数. ……………………………7分
(1 ,3)时,f(x)是减函数. ……………………………7分
⑵
.files/image196.gif)
当.files/image198.gif) 时,
时,.files/image187.gif) 当
当.files/image189.gif) 时,
时,.files/image191.gif) 当
当.files/image201.gif) 时,
时,.files/image187.gif)
又.files/image208.gif) 时,
时, .files/image095.gif) 的最小值为
的最小值为
对任意.files/image210.gif) 恒成立
恒成立.files/image212.gif) …………11分
…………11分
19解:(I)当.files/image218.gif) 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了.files/image220.gif) 小时,…………2分
小时,…………2分
要耗没.files/image222.gif) (升)。…………4分
(升)。…………4分
答:当汽车以
(II)当速度为.files/image117.gif) 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了.files/image224.gif) 小时,…………6分,设耗油量为
小时,…………6分,设耗油量为.files/image226.gif) 升,依题意得
升,依题意得.files/image228.gif) …………8分
…………8分
.files/image230.gif) 令
令.files/image232.gif) 得
得.files/image234.gif) …………10分
…………10分
当.files/image236.gif) 时,
时,.files/image238.gif) 是减函数; 当
是减函数; 当.files/image240.gif) 时,
时,.files/image242.gif) 是增函数。
是增函数。
因为.files/image226.gif) 在
在.files/image251.gif) 上只有一个极值,所以它是最小值。…………12分
上只有一个极值,所以它是最小值。…………12分
答:当汽车以
20解:(1).files/image253.gif) ……………………………………2分
……………………………………2分
当.files/image261.gif) 时,
时,.files/image263.gif) ,所以
,所以.files/image265.gif) 是函数的递减区间;…………5分
是函数的递减区间;…………5分
(2)令.files/image273.gif) 则
则.files/image275.gif) ,
,
.files/image277.gif) ………………………………………………10分
………………………………………………10分
当.files/image125.gif) 时,
时,.files/image280.gif) ,所以
,所以.files/image282.gif) 在(1,+∞)上为增函数。………………………12分
在(1,+∞)上为增函数。………………………12分
所以当.files/image125.gif) 时,
时, .files/image284.gif) ,………………………13分
,………………………13分
21解:(1)令F(x)=f(x)-g(x)=x3+(2-a)x2+4,
∴f(x)≥g(x)在[0,+∞)上恒成立等价于F(x)min≥0(x∈[0,+∞)). ………………………1分
F′(x)= 3x2+2(2-a)x,
①若2-a≥0,即a≤2时, .files/image290.gif) F(x)在[0,+∞)是增函数,F(x)min=4>0; ………3分
F(x)在[0,+∞)是增函数,F(x)min=4>0; ………3分
②若2-a<0,即a>2时,F′(x)=3x2-2(a-2)x=3x[x-.files/image292.gif) ].由于F′(
].由于F′(.files/image294.gif) )=0,
)=0,
且当x>.files/image294.gif) 时,F′(x)>0;当0≤x<
时,F′(x)>0;当0≤x<.files/image294.gif) 时,F(x)min=F(
时,F(x)min=F(.files/image294.gif) )≥0, ………………………6分
)≥0, ………………………6分
即(.files/image294.gif) )3-(a-2)(
)3-(a-2)(
.files/image295.gif) )2+4≥0,得a≤5.∴2<a≤5.又a≤2, ………………………7分
)2+4≥0,得a≤5.∴2<a≤5.又a≤2, ………………………7分
取并集得a的取值范围是(-∞,5]. ………………………8分
(2)由题意f(x)min≥g(x)max,x∈[0,+∞).
x∈[0,+∞)时.files/image297.gif) 显然,f(x)min=-4(当x=0时,取最小值). ………………10分
显然,f(x)min=-4(当x=0时,取最小值). ………………10分
∵a≥0时,g(x)图像开口向上,无最大值,不合题意, ………………………11分
∴a<0.又∵-.files/image299.gif) ∈[0,+∞),g(x)max=-
∈[0,+∞),g(x)max=-.files/image301.gif) , ………………………13分
, ………………………13分
∴-.files/image301.gif) ≤-4.∴a≤-
≤-4.∴a≤-.files/image303.gif) .∴a的取值范围是(-∞,-
.∴a的取值范围是(-∞,-.files/image303.gif) ]. ………………………14分
]. ………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com