
题目列表(包括答案和解析)
 九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.
九年义务教育三年制初级中学教科书代数第三册中,有以下几段文字:“对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y)和它对应;对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M和它对应,也就是说,坐标平面内的点与有序实数对是一一对应的.”“一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.”“实际上,所有一次函数的图象都是一条直线.”“因为两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线,就可以了.”由此可知:满足函数关系式的有序实数对所对应的点,一定在这个函数的图象上;反之,函数图象上的点的坐标,一定满足这个函数的关系式.另外,已知直线上两点的坐标,便可求出这条直线所对应的一次函数的解析式.如图,在直角坐标系中, 是原点,
是原点, 三点的坐标分别
三点的坐标分别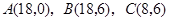 ,四边形
,四边形 是梯形,点
是梯形,点 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿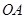 向终点
向终点 运动,速度为每秒
运动,速度为每秒 个单位,点
个单位,点 沿
沿 向终点
向终点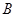 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.

(1)求直线 的解析式.
的解析式.
(2)设从出发起,运动了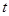 秒.如果点
秒.如果点 的速度为每秒
的速度为每秒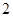 个单位,试写出点
个单位,试写出点 的坐标,并写出此时
的坐标,并写出此时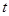 的取值范围.
的取值范围.
(3)设从出发起,运动了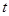 秒.当
秒.当 ,
, 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形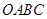 的周长的一半,这时,直线
的周长的一半,这时,直线 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出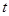 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
【解析】(1)根据待定系数法就可以求出直线OC的解析式(2)本题应分Q在OC上,和在CB上两种情况进行讨论.即0≤t≤5和5<t≤10两种情况(3)P、Q两点运动的路程之和可以用t表示出来,梯形OABC的周长就可以求得.当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,就可以得到一个关于t的方程,可以解出t的值.梯形OABC的面积可以求出,梯形OCQP的面积可以用t表示出来.把t代入可以进行检验
如图,在直角坐标系中,![]() 是原点,
是原点,![]() 三点的坐标分别
三点的坐标分别![]() ,四边形
,四边形![]() 是梯形,点
是梯形,点![]() 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点![]() 沿
沿![]() 向终点
向终点![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位,点
个单位,点![]() 沿
沿![]() 向终点
向终点![]() 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.

(1)求直线![]() 的解析式.
的解析式.
(2)设从出发起,运动了![]() 秒.如果点
秒.如果点![]() 的速度为每秒
的速度为每秒![]() 个单位,试写出点
个单位,试写出点![]() 的坐标,并写出此时
的坐标,并写出此时![]() 的取值范围.
的取值范围.
(3)设从出发起,运动了![]() 秒.当
秒.当![]() ,
,![]() 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形![]() 的周长的一半,这时,直线
的周长的一半,这时,直线![]() 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出![]() 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
【解析】(1)根据待定系数法就可以求出直线OC的解析式(2)本题应分Q在OC上,和在CB上两种情况进行讨论.即0≤t≤5和5<t≤10两种情况(3)P、Q两点运动的路程之和可以用t表示出来,梯形OABC的周长就可以求得.当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半,就可以得到一个关于t的方程,可以解出t的值.梯形OABC的面积可以求出,梯形OCQP的面积可以用t表示出来.把t代入可以进行检验
近年来,大学生就业日益困难.为了扶持大学生自主创业,某市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其他费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
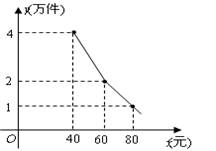
(1)分别求出40<x≤60;60<x<80时,月销售量y(万件)与销售
单价x(元)之间的函数关系;
(2)当销售单价定为50元时,为保证公司月利润达到5万元
可安排员工多少人?
(3)若该公司有80名员工,则该公司最早可在几月后还清贷款?
【解析】(1)利用图象上点的坐标利用待定系数法代入y=kx+b,求出一次函数解析式即可;
(1) 根据利润=销售额—生产成本—员工工资—其它费用列方程求出解
(3)分两种情况进行讨论:当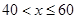 时,当
时,当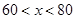 时得出结论
时得出结论
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com