练习册

  • 练习册
  • 试题
    2．函数值域的求法:①分析法 ,②配方法 ,③判别式法 ,④利用函数单调性 ,⑤换元法 , ⑥利用均值不等式 , ⑦利用数形结合或几何意义(斜率.距离. 绝对值的意义等),⑧利用函数有界性(..等),⑨平方法,⑩ 导数法 【查看更多】

     

    题目列表(包括答案和解析)

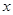    对函数作=h(t)的代换，则不改变函数值域的代换是（    ）

    A、h(t)=10t          B、h(t)=t2        C、h(t)=sint       D、h(t)=log2t

     

    查看答案和解析>>

    函数零点的求法

    求函数y＝f(x)的零点：

    (1)代数法：求方程f(x)＝0的________；

    (2)几何法：对于不能用求根公式的方程，可以将它与函数y＝f(x)的图象联系起来，并利用________找出零点．

    查看答案和解析>>

    对函数作=h（t）的代换，则不改变函数值域的代换是（    ）

           A．h（t）=10t          B．h（t）=t2            C．h（t）=sint           D．h（t）=log2t

    查看答案和解析>>

    已知△ABC的三内角A、B、C的对边分别是a，b，c，面积为S△ABC，且
    m
    =(b2+c2-a2，-2)，
    n
    =(sinA，S△ABC)    ，
    m
    ⊥
    n
    ．
    （1）求函数f(x)=4cosxsin(x-
    A
    2
    )    在区间[0，
    π
    2
    ]上的值域；
    （2）若a=3，且sin(B+
    π
    3
    )=
    		3
    3
    ，求b．

    查看答案和解析>>

    已知向量a=（1，sinx+
    		3
    cosx），b=（1，y），若a∥b且有函数y=f（x）．
    （I）若x∈[-
    π
    6
    ，
    π
    3
    ]，求函数y=f（x）的值域；
    （II）已知锐角△ABC的三内角分别是A、B、C，若有f（A-
    π
    3
    )=
    		3
    ，边BC=
    		7
    ，sinB=
    		21
    7
    ，求边AC的长．

    查看答案和解析>>


    同步练习册答案