
题目列表(包括答案和解析)
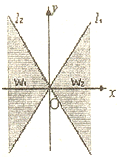 如图,直线ll:y=2x与直线l2:y=-2x之间的阴影区域(不含边界)记为w,其左半部分记为w1,右半部分记为W2.
如图,直线ll:y=2x与直线l2:y=-2x之间的阴影区域(不含边界)记为w,其左半部分记为w1,右半部分记为W2.| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
 ,
, )】
)】
(2)对λ的讨论:?
①点P在![]() 上(但不与B重合)时,λ .特别地,当λ=0时,P与A ;λ=1时,P是
上(但不与B重合)时,λ .特别地,当λ=0时,P与A ;λ=1时,P是![]() 的 ,得 坐标公式:x= , y= .?
的 ,得 坐标公式:x= , y= .?
②点P在![]() 的延长线上时,λ .?
的延长线上时,λ .?
③点P在![]() 的延长线(即
的延长线(即![]() 的反向延长线)上时, .?
的反向延长线)上时, .?
(3)三角形重心坐标公式:△ABC中,A(x1,y1),B(x2,y2),C(x3,y3),重心G(x,y),则有x= ,y= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com