
题目列表(包括答案和解析)
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
D
解析:当x>0时,![]() ,即
,即![]() 令
令![]() ,
,
则函数![]() 在区间(0,+∞)上为减函数,又
在区间(0,+∞)上为减函数,又![]() 在定义域上是奇函数,
在定义域上是奇函数,
∴函数![]() 在定义域上是偶函数,且
在定义域上是偶函数,且![]() ,则
,则![]() >0在(0,+∞)上的解集是(0,2);
>0在(0,+∞)上的解集是(0,2);
函数![]() 是定义域上的奇函数,则
是定义域上的奇函数,则![]() >0的解集是(-∞,-2)∪(0,2).
>0的解集是(-∞,-2)∪(0,2).
D
解析:当x>0时,![]() ,即
,即![]() 令
令![]() ,
,
则函数![]() 在区间(0,+∞)上为减函数,又
在区间(0,+∞)上为减函数,又![]() 在定义域上是奇函数,
在定义域上是奇函数,
∴函数![]() 在定义域上是偶函数,且
在定义域上是偶函数,且![]() ,则
,则![]() >0在(0,+∞)上的解集是(0,2);
>0在(0,+∞)上的解集是(0,2);
函数![]() 是定义域上的奇函数,则
是定义域上的奇函数,则![]() >0的解集是(-∞,-2)∪(0,2).
>0的解集是(-∞,-2)∪(0,2).
D
解析:当x>0时,![]() ,即
,即![]() 令
令![]() ,
,
则函数![]() 在区间(0,+∞)上为减函数,又
在区间(0,+∞)上为减函数,又![]() 在定义域上是奇函数,
在定义域上是奇函数,
∴函数![]() 在定义域上是偶函数,且
在定义域上是偶函数,且![]() ,则
,则![]() >0在(0,+∞)上的解集是(0,2);
>0在(0,+∞)上的解集是(0,2);
函数![]() 是定义域上的奇函数,则
是定义域上的奇函数,则![]() >0的解集是(-∞,-2)∪(0,2).
>0的解集是(-∞,-2)∪(0,2).
研究问题:“已知关于 的不等式
的不等式 的解集为(1,2),解关于
的解集为(1,2),解关于 的不等式
的不等式 ”,有如下解法:
”,有如下解法:
解:由

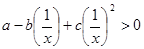 令
令 ,则
,则
所以不等式 的解集为
的解集为
参考上述解法,已知关于x的不等式 的解集为(-3,-1)∪(2,3),
的解集为(-3,-1)∪(2,3),
则关于x的不等式 的解集为 .
的解集为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com