练习册

  • 练习册
  • 试题
    14．如图所示.一带电粒子垂直射人匀强电场.经电场偏转后从磁场的左边界上A点进入垂直纸面向外的匀强磁场中.最后从磁场的左边界上的B点离开磁场.已知:带电粒子比荷=3.2×109C／kg.电场强度E=200 V／m.磁感应强度B=2．5×10-2T.金属板长L=25 cm.粒子初速度v0=4×105 m／s.求:A.B之间的距离. 【查看更多】

     

    题目列表(包括答案和解析)

    如图所示，一带电粒子垂直射人匀强电场，经电场偏转后从磁场的左边界上A点进入垂直纸面向外的匀强磁场中，最后从磁场的左边界上的B点离开磁场。已知：带电粒子比荷=3.2×109C／kg，电场强度E=200 V／m，磁感应强度B=2.5×10-2T，金属板长L=25 cm，粒子初速度vb=4×105 m／s。求：A、B之间的距离。(带电粒子重力忽略不计)

    查看答案和解析>>

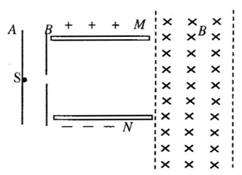
    如图所示，一质量为m、电荷量为+q、重力不计的带电粒子，从A板的S点由静止开始释放，经A、B加速电场加速后，穿过中间偏转电场，再进人右侧匀强磁场区域.已知AB间的电压为U，MN极板间的电压为2U，MN两板间的距离和板长均为L，磁场垂直纸面向里、磁感应强度为B、有理想边界.求：

    (1) 带电粒子离幵B板时速度V0的大小；

    (2) 带电粒子离开偏转电场时速度V的大小与方向；

    (3) 要使带电粒子最终垂直磁场右边界射出磁场，磁场的宽度d多大？

     

    查看答案和解析>>

    如图所示，一质量为m、电荷量为+q、重力不计的带电粒子，从A板的S点由静止开始释放，经A、B加速电场加速后，穿过中间偏转电场，再进人右侧匀强磁场区域.已知AB间的电压为U，MN极板间的电压为2U，MN两板间的距离和板长均为L，磁场垂直纸面向里、磁感应强度为B、有理想边界.求：

    (1) 带电粒子离幵B板时速度V0的大小；

    (2) 带电粒子离开偏转电场时速度V的大小与方向；

    (3) 要使带电粒子最终垂直磁场右边界射出磁场，磁场的宽度d多大？[来源:Zxxk.Com]

     

    查看答案和解析>>

    如图所示，一质量为m、电荷量为+q、重力不计的带电粒子，从A板的S点由静止开始释放，经A、B加速电场加速后，穿过中间偏转电场，再进人右侧匀强磁场区域．已知AB间的电压为U，MN极板间的电压为2U，MN两板间的距离和板长均为L，磁场垂直纸面向里、磁感应强度为B、有理想边界．求：

    （1） 带电粒子离幵B板时速度V0的大小；

    （2） 带电粒子离开偏转电场时速度V的大小与方向；

    （3） 要使带电粒子最终垂直磁场右边界射出磁场，磁场的宽度d多大？

    查看答案和解析>>

    如图所示，虚线为相邻两个匀强磁场区域1和区域2的边界，磁场的方向都垂直纸面向里．区域1的磁感应强度的大小为B，区域2的磁感应强度的大小为3B/4．两个磁场区域的宽度都是d，一质量为m、电量为q的粒子，沿垂直于区域1边界的初速从A点射人区域1并进入区域2，最后恰好未能穿出区域2，求此带电粒子的速度．（不计粒子重力．）

    查看答案和解析>>

    1.C  2.A   3. BD   4.BD   5. B   6. BC  7.BD  8. A  9. B   10.AD

     

    11.答案：（16分）

    （1）  (6分)（2）①a；(4分)②2547；5094；(各3分)

    12． 解：

    　　（1）由牛顿第二定律：

    　　  (4分)

    　　（2）跳伞员最后匀速运动：  (3分)

    　　（3）损失的机械能：  (3分)

     

    13.解答：弹性环下落到地面时，速度大小为v1,由动能定理得

    Mgl-fl=Mv12/2                                   (3分)

    解得v1=4 m/s                                   （1分）

    弹性环反弹后被直棒刺卡住时，与直棒速度相同，设为v2,由动量守恒定律得

    Mv1=(M+m)v2                                                (3分)

    解得v2=3 m/s                              （1分）

    直棒能上升的最大高度为

    H=v22/2g=0.45 m                             （2分）．

    14.(12分)

    解：在电场中：加速度a=，  ①   1分

    运动时间t=，  ②                1分

    偏出电场时的竖直分速度vy=at  ③    1分

    速度偏向角tanθ=，  ④           1分

    由以上各式，代入数据解得：

    tanθ=1．  ∴θ=45°  ⑤               1分

    粒子射出电场时运动速度大小v=  ⑥      2分

    在磁场中：

    向心力满足qvB=m  ⑦                  2分

    ∴r=由几何关系得r  ⑧         1分

    由以上各式，代人数据解得=10-2 m  ⑨     2分

    评分参考：①、②、③、④、⑤、⑧各式均为1分，⑥、⑦、⑨式各2分；其他方法结果正确也给分。

    15．解：(1)小球从开始自由下落到到达管口B的过程中机械能守恒，故有：

                                                            (2分)

    到达B点时速度大小为                                            (2分)

    (2)设电场力的竖直分力为Fy、，水平分力为Fx，则Fy=mg(方向竖直向上).小球从B运动到C的过程中，由动能定理得：                              (1分)

    小球从管口C处脱离圆管后，做类平抛运动，由于其轨迹经过A点，有

                                                                  (1分)

                                                          (1分)

    联立解得：Fx=mg                                                

    电场力的大小为：                                  (1分)

     (3)小球经过管口C处时，向心力由Fx和圆管的弹力N提供，设弹力N的方向向左，则

                                                                 (2分)

      解得：N=3mg(方向向左)                                             (1分)

    根据牛顿第三定律可知，小球经过管口C处时对圆管的压力为

        ，方向水平向右                                            (1分)

     


    同步练习册答案