
题目列表(包括答案和解析)
| 2 |
| 3 |
| 1 |
| 2 |
(1)共有多少种不同的结果?
(2)其中向上数字之和是5的有多少种?
(3)出现点数相同的概率.
(4)出现的点数和为奇数的概率.
(5)出现点数和为奇数且先奇后偶的概率.
(6)若抛掷三枚骰子,则出现点数都相同的概率为多少?
(7)若以连续投掷两枚骰子分别得到的点数m、n作为点P的坐标(m,n),求点P落在圆x2+y2=16内的概率.
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投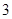 次:在
次:在 处每投进一球得
处每投进一球得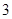 分,在
分,在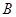 处每投进一球得
处每投进一球得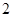 分;如果前两次得分之和超过
分;如果前两次得分之和超过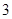 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在 处的命中率
处的命中率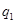 为
为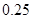 ,在
,在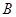 处的命中率为
处的命中率为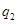 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在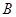 处投,用
处投,用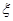 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
0 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
(1) 求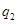 的值;
的值; (2)
求随机变量
(2)
求随机变量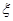 的数学期望
的数学期望 ;
;
(3) 试比较该同学选择都在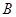 处投篮得分超过
处投篮得分超过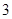 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过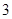 分的概率的大小.
分的概率的大小.
(02年全国卷文)(本小题满分12分,附加题满分4分)
(I)给出两块相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;
(II)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;
(III)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分)
如果给出的是一块任意三角形的纸片(如图3),要求剪成一个直三棱柱,使它的全面积与给出的三角形的面积相等。请设计一种剪拼方法,用虚线标示在图3中,并作简要说明。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com