练习册

  • 练习册
  • 试题
    12．已知点P1(a1.b1).P2(a2.b2).-.Pn(an.bn)(n∈N*)都在函数y＝logx的图象上． (1)若数列{bn}是等差数列.求证:数列{an}为等比数列, (2)若数列{an}的前n项和为Sn＝1-2-n.过点Pn.Pn+1的直线与两坐标轴所围成的三角形面积为cn.求使cn≤t对n∈N*恒成立的实数t的取值范围． 解:(1)因为数列{bn}是等差数列.故设公差为d. 则bn+1-bn＝d对n∈N*恒成立． 依题意bn＝logan.an＝()bn. 由an>0.所以＝()bn+1-bn＝()d是定值.从而数列{an}是等比数列． (2)当n＝1时.a1＝S1＝.当n≥2时.an＝Sn-Sn-1＝()n.当n＝1时也适合此式.即数列{an}的通项公式是an＝()n. 由bn＝logan.数列{bn}的通项公式是bn＝n. 所以Pn(.n).Pn+1(.n+1).过这两点的直线方程是y-n＝-2n+1(x-).该直线与坐标轴的交点是An(.0)和Bn(0.n+2)． cn＝|OAn|×|OBn|＝. 因为cn-cn+1＝-＝>0. 即数列{cn}的各项依次单调递减.所以要使cn≤t对n∈N*恒成立.只需c1≤t.又c1＝.可得t的取值范围是[.+∞)． 故实数t的取值范围是[.+∞)． 【查看更多】

     

    题目列表(包括答案和解析)

    2009年春季，我国部分地区H1N1流行，党和政府采取果断措施，防治结合，很快使病情得到控制．下表是某同学记载的5月1号到5月12号每天北京市H1N1病治愈者数据，根据这些数据绘制散点图．
    日期 5.1 5.2 5.3 5.4 5.5 5.6
    人数 100 109 115 118 121 134
    日期 5.7 5.8 5.9 5.10 5.11 5.12
    人数 141 152 168 175 186 203
    下列说法正确的个数有（　　）
    ①根据此散点图，可以判断日期与人数具有线性相关关系；
    ②根据此散点图，可以判断日期与人数具有一次函数关系；
    ③后三天治愈出院的人数占这12天治愈出院人数的30%多；
    ④后三天中每天治愈出院的人数均超过这12天内北京市H1N1病愈者总人数的20%．

    查看答案和解析>>

    （2009•台州二模）如图，已知A、B、C是一条直路上的三点，一个人从A出发行走到B处时，望见塔M（将塔M视为与A、B、C在同一水平面上一点）在正东方向且A在东偏南α方向，继续行走1km在到达C处时，望见塔M在东偏南β方向，则塔M到直路ABC的最短距离为（　　）

    查看答案和解析>>

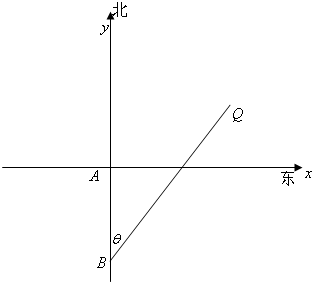    （2009•奉贤区一模）A岛正南40海里处的洋面B上有一条走私船．它正以10
    		5
    海里/小时的速度朝北偏东θ(θ=arctan
    1
    2
    )    的方向作匀速直线方向逃走．3小时后有关部门接到报警并派辑私船从A岛出发追击走私船．如图所示，建立平面直角坐标系，
    （1）写出3小时后走私船Q1的坐标以及t小时后走私船Qt的坐标
    （2）已知辑私船的最大航速度为40
    		2
    海里/小时，并假设走私船在逃走时不改变它的航向，辑私船沿什么方向行驶才能最快截获走私船？并求出所需时间?

    查看答案和解析>>

    2009年2月26日，在亚丁湾海域执行护航任务的中国海军“海口”舰，成功营救一艘意大利商船.

    假设当日，我“海口”舰接到位于北偏东30°方向距我舰10海里的友舰发出的信号，报告在他们正东20海里处有一艘意大利商船遇险，我“海口”舰立即紧急前往营救，试问我“海口”舰应朝北偏东多少度的方向沿直线前往该艘意大利商船处救援（参考数据）

    查看答案和解析>>

     (北京市东城区2009年3月高中示范校高三质量检测文)已知，则=                            （　 ）

    A.             B.             C.               D.  

    查看答案和解析>>


    同步练习册答案