(1)求两木板对木块施加的静摩擦力的大小及方向;

(2)若左右两边加在木板上的压力均变为2F，两木板对木块的摩擦力如何变化?

(3)若左右两边的压力保持F不变，而使整个装置沿水平、竖直等方向匀速运动，木块所受的静摩擦力的大小如何?方向如何?关于摩擦力方向跟物体运动方向的关系，能得出什么结论?

如图所示，在竖直平面内建立xOy直角坐标系，Oy表示竖直向上的方向．已知该平面内x轴上方的区域存在沿x轴负方向足够大的匀强电场，场强E₁=1000N/C，现有一个质量m=0.05kg、带电量为2.5×10^-4C 的小球从坐标原点O沿y轴正方向以某一初速度v₀竖直向上抛出，它到达最高点后(图中未画出)，再落回x轴上的P（6.4，0）点，不计空气阻力，g取10 m/s².请回答下列问题：

（1）小球带何种电荷；

（2）小球从O点抛出到落回x轴的过程中电势能的改变量;

（3）小球上升的最大高度及初速度v₀;

（4）若要使小球通过P点后作直线运动，则在x轴下方所加匀强电场E₂的最小值及方向。

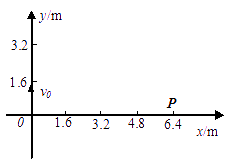
如图9-3-9所示，间距l＝0.3 m的平行金属导轨a₁b₁c₁和a₂b₂c₂分别固定在两个竖直面内．在水平面a₁b₁b₂a₂区域内和倾角θ＝37°的斜面c₁b₁b₂c₂区域内分别有磁感应强度B₁＝0.4 T，方向竖直向上和B₂＝1 T、方向垂直于斜面向上的匀强磁场．电阻R＝0.3 Ω、质量m₁＝0.1 kg、长为l的相同导体杆K、S、Q分别放置在导轨上，S杆的两端固定在b₁、b₂点，K、Q杆可沿导轨无摩擦滑动且始终接触良好．一端系于K杆中点的轻绳平行于导轨绕过轻质定滑轮自然下垂，绳上穿有质量m₂＝0.05 kg的小环．已知小环以a＝6 m/s²的加速度沿绳下滑，K杆保持静止，Q杆在垂直于杆且沿斜面向下的拉力F作用下匀速运动．不计导轨电阻和滑轮摩擦，绳不可伸长．取g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8.求

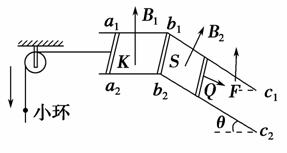
图9-3-9

(1)小环所受摩擦力的大小；

(2)Q杆所受拉力的瞬时功率．

（13分）如图所示，在竖直平面内有一平面直角坐标系xoy,第一、四象限内存在大小相等方向相反且平行于y轴的匀强电场。在第四象限内某点固定一个点电荷Q（假设该点电荷对第一象限内的电场无影响）。现有一质量为m=9×10^-4kg，带电量为 q=3×10^-12C的带电微粒从y轴上A 点（y=0.9cm）以初速度v₀=0.8m/s垂直y轴射入第一象限经x轴上的B点进入第四象限做匀速圆周运动且轨迹与y轴相切（图中A、B及点电荷Q的位置均未标出）。不考虑以后的运动。（重力加速度g=10m／s²，静电力常量k=9.0×10⁹Nm/C^2、，^、sin37°=0．6，cos37°=0．8）

试求：（1）点电荷通过B的速度(要求画出带点微粒运动轨迹）
（2）点电荷Q的电荷量