
题目列表(包括答案和解析)
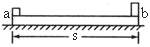
如图,长木板ab的b端固定一挡板,木板连同挡板的质量M=4.0kg,a、b间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速υο=4.0·s-1沿木板向前滑动,直到和挡板相连.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
![]()
![]()
 如图,长木板ab的b端固定一档板,木板连同挡板的质量为M=4.0kg,a到挡板的距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和档板相撞.g=10m/s2
如图,长木板ab的b端固定一档板,木板连同挡板的质量为M=4.0kg,a到挡板的距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和档板相撞.g=10m/s2
(2004年全国理综卷Ⅲ)如图,长木板ab的b端固定一挡板,木板连同挡板的质量为M=4.0kg,a、b间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速 沿木板向前滑动,直到和挡板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
沿木板向前滑动,直到和挡板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com