
题目列表(包括答案和解析)
(05年广东卷)(14分)
在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1,![]() 、
、![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() 点与坐标原点重合(如图5所示).将矩形折叠,使
点与坐标原点重合(如图5所示).将矩形折叠,使![]() 点落在线段
点落在线段![]() 上.
上.
(Ⅰ)若折痕所在直线的斜率为![]() ,试写出折痕所在直线的方程;
,试写出折痕所在直线的方程;
(Ⅱ)求折痕的长的最大值.

(05年广东卷)(12分)
化简![]() 并求函数
并求函数![]() 的值域和最小正周期.
的值域和最小正周期.
(05年广东卷)(12分)
箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量比为![]() .现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n次.以
.现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过n次.以![]() 表示取球结束时已取到白球的次数.
表示取球结束时已取到白球的次数.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)求![]() 的数学期望.
的数学期望.
(05年广东卷)(14分)
设函数![]() 在
在![]() 上满足
上满足![]() ,
,![]() ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有![]() .
.
(Ⅰ)试判断函数![]() 的奇偶性;
的奇偶性;
(Ⅱ)试求方程![]() 在闭区间
在闭区间![]() 上的根的个数,并证明你的结论.
上的根的个数,并证明你的结论.
(05年广东卷)(14分)
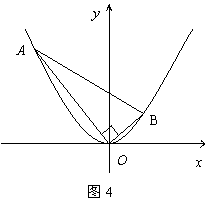
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 上异于坐标原点
上异于坐标原点![]() 的两不同动点A、B满足
的两不同动点A、B满足![]() (如图4所示)
(如图4所示)
(Ⅰ)求![]() 得重心
得重心![]() (即三角形三条中线的交点)
(即三角形三条中线的交点)
的轨迹方程;
(Ⅱ)![]() 的面积是否存在最小值?若存在,请求出
的面积是否存在最小值?若存在,请求出
最小值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com