
题目列表(包括答案和解析)
(1)证明直线和平面垂直的判定定理,即已知:如图1,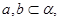 且
且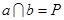 ,
, 求证:
求证: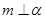
(2)请用直线和平面垂直的判定定理证明:如果一条直线垂直于两个平行平面中的一个,那么它也垂直于另一个平面,即
已知:如图2,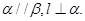 求证:
求证: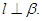


直线与平面垂直的判定定理 如果一条直线和平面内的两条_________直线垂直,那么这条直线_________于这个平面.
将直线与平面垂直的判定定理“如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面”用符号语言表示为
A.m![]() α,m∩n=B,l⊥n,l⊥m
α,m∩n=B,l⊥n,l⊥m![]() l⊥α
l⊥α
B.m![]() α,n
α,n![]() α,m∩n=B,l⊥m,l⊥n
α,m∩n=B,l⊥m,l⊥n![]() l⊥α
l⊥α
C.m![]() α,n
α,n![]() α,m∩n=B
α,m∩n=B![]() l⊥n,l⊥m,l⊥α
l⊥n,l⊥m,l⊥α
D.m![]() α,n
α,n![]() α,l⊥m,l⊥n
α,l⊥m,l⊥n![]() l⊥α
l⊥α
由平面与平面垂直的判定定理知如果m为平面α内的
一条直线,![]() ,则
,则![]() ,反过来则不一定.所以“
,反过来则不一定.所以“![]() ”是“
”是“![]() ”的必要不充分条件. w.w.w.k.s.5.u.c.o.m
”的必要不充分条件. w.w.w.k.s.5.u.c.o.m ![]()
![]()
答案:B.
【命题立意】:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.
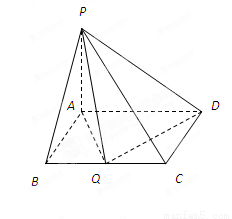
在四棱锥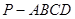 中,
中,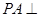 平面
平面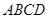 ,底面
,底面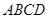 为矩形,
为矩形,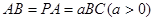 .
.
(Ⅰ)当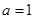 时,求证:
时,求证: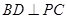 ;
;
(Ⅱ)若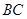 边上有且只有一个点
边上有且只有一个点 ,使得
,使得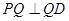 ,求此时二面角
,求此时二面角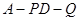 的余弦值.
的余弦值.
【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,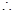
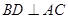
又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使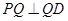 ,只要
,只要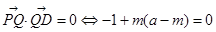
所以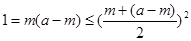 ,即
,即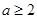 ………6分
………6分
由此可知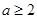 时,存在点Q使得
时,存在点Q使得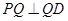
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得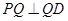
由此知道a=2, 设平面POQ的法向量为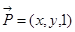
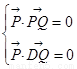 ,所以
,所以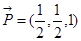 平面PAD的法向量
平面PAD的法向量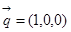
则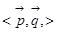 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以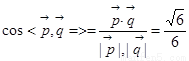
因此二面角A-PD-Q的余弦值为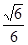
解:(Ⅰ)当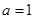 时,底面ABCD为正方形,
时,底面ABCD为正方形,
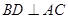
又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使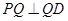 ,只要
,只要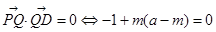
所以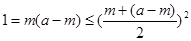 ,即
,即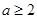 ………6分
………6分
由此可知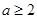 时,存在点Q使得
时,存在点Q使得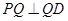
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得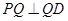 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为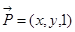
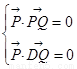 ,所以
,所以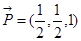 平面PAD的法向量
平面PAD的法向量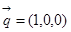
则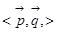 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以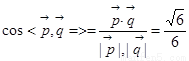
因此二面角A-PD-Q的余弦值为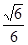
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com