练习册

  • 练习册
  • 试题
    24． 已知:如图①.在中....点由出发沿方向向点匀速运动.速度为1cm/s,点由出发沿方向向点匀速运动.速度为2cm/s,连接．若设运动的时间为().解答下列问题:(1)当为何值时.? (2)设的面积为().求与之间的函数关系式, (3)是否存在某一时刻.使线段恰好把的周长和面积同时平分?若存在.求出此时的值,若不存在.说明理由, (4)如图②.连接.并把沿翻折.得到四边形.那么是否存在某一时刻.使四边形为菱形?若存在.求出此时菱形的边长,若不存在.说明理由． 24． 解:(1)在Rt△ABC中.. 由题意知:AP = 5-t.AQ = 2t. 若PQ∥BC.则△APQ ∽△ABC. ∴. ∴. ∴． ··································································································· 3′ (2)过点P作PH⊥AC于H． ∵△APH ∽△ABC. ∴. ∴. ∴. ∴． ··········································· 6′ (3)若PQ把△ABC周长平分. 则AP+AQ=BP+BC+CQ． ∴. 解得:． 若PQ把△ABC面积平分. 则. 即-+3t=3． ∵ t=1代入上面方程不成立. ∴不存在这一时刻t.使线段PQ把Rt△ACB的周长和面积同时平分．················ 9′ (4)过点P作PM⊥AC于M.PN⊥BC于N. 若四边形PQP ′ C是菱形.那么PQ＝PC． ∵PM⊥AC于M. ∴QM=CM． ∵PN⊥BC于N.易知△PBN∽△ABC． ∴. ∴. ∴. ∴. ∴. 解得:． ∴当时.四边形PQP ′ C 是菱形． 此时. . 在Rt△PMC中.. ∴菱形PQP ′ C边长为． 12′ 3326． 在等边中.点为上一点.连结.直线与分别相交于点.且． (1)如图1.写出图中所有与相似的三角形.并选择其中一对给予证明, (2)若直线向右平移到图2.图3的位置时中的结论是否仍然成立?若成立.请写出来.若不成立.请说明理由, (3)探究:如图1.当满足什么条件时.?请写出探究结果.并说明理由． (说明:结论中不得含有未标识的字母) 26． (1)与······························································ 2分 以为例.证明如下: ····································································································· 4分 (2)均成立.均为.········································· 6分 (3)平分时.．····································································· 7分 证明:平分 ··············································································································· 8分 又 ············································································································· 10分 注:所有其它解法均酌情赋分． 34 如图.点A(m.m+1).B(m+3.m-1)都在反比例函数的图象上． (1)求m.k的值, (2)如果M为x轴上一点.N为y轴上一点. 以点A.B.M.N为顶点的四边形是平行四边形. 试求直线MN的函数表达式． (3)选做题:在平面直角坐标系中.点P的坐标 为(5.0).点Q的坐标为(0.3).把线段PQ向右平 移4个单位.然后再向上平移2个单位.得到线段P1Q1. 则点P1的坐标为 .点Q1的坐标为 ． 24． 解:(1)由题意可知.． 解.得 m＝3． ------------3分 ∴ A(3.4).B(6.2), ∴ k＝4×3=12． -----------4分 (2)存在两种情况.如图: ①当M点在x轴的正半轴上.N点在y轴的正半轴 上时.设M1点坐标为(x1.0).N1点坐标为(0.y1)． ∵ 四边形AN1M1B为平行四边形. ∴ 线段N1M1可看作由线段AB向左平移3个单位. 再向下平移2个单位得到的(也可看作向下平移2个单位.再向左平移3个单位得到的)． 由(1)知A点坐标为(3.4).B点坐标为(6.2). ∴ N1点坐标为.即N1(0.2), ------------5分 M1点坐标为.即M1(3.0)． ------------6分 设直线M1N1的函数表达式为.把x＝3.y＝0代入.解得． ∴ 直线M1N1的函数表达式为． --------------8分 ②当M点在x轴的负半轴上.N点在y轴的负半轴上时.设M2点坐标为(x2.0).N2点坐标为(0.y2)． ∵ AB∥N1M1.AB∥M2N2.AB＝N1M1.AB＝M2N2. ∴ N1M1∥M2N2.N1M1＝M2N2． ∴ 线段M2N2与线段N1M1关于原点O成中心对称． ∴ M2点坐标为.N2点坐标为． ---------9分 设直线M2N2的函数表达式为.把x＝-3.y＝0代入.解得. ∴ 直线M2N2的函数表达式为． 所以.直线MN的函数表达式为或． ------11分 ． ------------------2分 35 如图.在梯形ABCD中.AB∥CD.AB＝7.CD＝1.AD＝BC＝5．点M.N分别在边AD.BC上运动.并保持MN∥AB.ME⊥AB.NF⊥AB.垂足分别为E.F． (1)求梯形ABCD的面积, (2)求四边形MEFN面积的最大值． (3)试判断四边形MEFN能否为正方形.若能. 求出正方形MEFN的面积,若不能.请说明理由． 25． 解:(1)分别过D.C两点作DG⊥AB于点G.CH⊥AB于点H． -----1分 ∵ AB∥CD. ∴ DG＝CH.DG∥CH． ∴ 四边形DGHC为矩形.GH＝CD＝1． ∵ DG＝CH.AD＝BC.∠AGD＝∠BHC＝90°. ∴ △AGD≌△BHC(HL)． ∴ AG＝BH＝＝3． ---2分 ∵ 在Rt△AGD中.AG＝3.AD＝5. ∴ DG＝4． ∴ ． ------------------3分 (2)∵ MN∥AB.ME⊥AB.NF⊥AB. ∴ ME＝NF.ME∥NF． ∴ 四边形MEFN为矩形． ∵ AB∥CD.AD＝BC. ∴ ∠A＝∠B． ∵ ME＝NF.∠MEA＝∠NFB＝90°. ∴ △MEA≌△NFB(AAS)． ∴ AE＝BF． --------4分 设AE＝x.则EF＝7-2x． -----5分 ∵ ∠A＝∠A.∠MEA＝∠DGA＝90°. ∴ △MEA∽△DGA． ∴ ． ∴ ME＝． ----------------------6分 ∴ ． --------8分 当x＝时.ME＝＜4.∴四边形MEFN面积的最大值为．-----9分 (3)能． --------------------------10分 由(2)可知.设AE＝x.则EF＝7-2x.ME＝． 若四边形MEFN为正方形.则ME＝EF． 即 7-2x．解.得 ． -----------------11分 ∴ EF＝＜4． ∴ 四边形MEFN能为正方形.其面积为． ---12分 3624． 如图.圆切轴于原点.过定点作圆切线交圆于点．已知.抛物线经过两点． (1)求圆的半径, (2)若抛物线经过点.求其解析式, (3)投抛物线交轴于点.若三角形为直角三角形.求点的坐标． 3725. 如图.抛物线交轴于A.B两点.交轴于M点.抛物线向右平移2个单位后得到抛物线.交轴于C.D两点. (1)求抛物线对应的函数表达式, (2)抛物线或在轴上方的部分是否存在点N.使以A.C.M.N为顶点的四边形是平行四边形.若存在.求出点N的坐标,若不存在.请说明理由, (3)若点P是抛物线上的一个动点.那么点P关于原点的对称点Q是否在抛物线上.请说明理由. 3825． 把一副三角板如图甲放置.其中...斜边.．把三角板DCE绕点C顺时针旋转15°得到△D1CE1．这时AB与CD1相交于点.与D1E1相交于点F． (1)求的度数, (2)求线段AD1的长, (3)若把三角形D1CE1绕着点顺时针再旋转30°得△D2CE2.这时点B在△D2CE2的内部.外部.还是边上?说明理由． 25． 解:(1)如图所示... ∴． ------------1分 又. ∴． ---3分 (2).∴∠D1FO=60°． .∴． ··································································· 4分 又..∴． .∴．····················································· 5分 又.∴． 在中.．································· 6分 (3)点在内部． ··········································································· 7分 理由如下:设交于点P.则． 在中.. ----·································· 9分 .即.∴点在内部． -----10分 【查看更多】

     

    题目列表(包括答案和解析)

    （2012•重庆模拟）“海上联合--2012”中俄海上联合演习于2012年4月22日起在山东青岛举行．据悉，此次中俄海上联合演习中俄双方会大约4000名官兵参加，将4000用科学记数法表示为
    4×103
    4×103
    ．

    查看答案和解析>>

    在一次环保知识测试中，三年一班的两名同学根据班级成绩（分数为整数）分别绘制了不同的频率分布直方图，如图1、2，已知图1从左到右每个小组的频率分别为0.04、0.08、0.24、0.32、0.20、0.12，其中68.5～76.5小组的频数为12；图2从左到右每个小组的频数之比为1：2：4：7：6：3：2，请结合条件和频率分布直方图回答下列问题：
    （1）三年一班参加测试的人数是多少？
    （2）若这次测试的成绩80分以上（含80分）为优秀，则优秀率是多少？
    （3）若这次测试的成绩60分以上（含60分0为及格，则及格率是多少？
    精英家教网精英家教网

    查看答案和解析>>

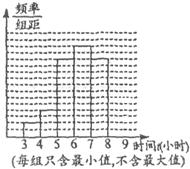    19、某校课外活动小组为了解本校九年级学生的睡眠时间情况，对学校若干名九年级学生的睡眠时间进行了抽查，将所得数据整理后，画出了频率分布直方图的一部分（如图所示）．根据全班睡眠时间统计共分为六个小组，图中从左至右前五个小组的频率分别是0.04，0.08，0.24，0.28，0.24，第二小组的频数为4．请回答：
    （1）这次被抽查的学生人数是多少？并补全频率分布直方图．
    （2）被抽查的学生中，睡眠时间在哪个范围内的人数最多？这一范围内的人数是多少？
    （3）如果该学校有900名九年级学生，若合理睡眠时间范围为7≤t＜9，那么请你估计一下这个学校九年级学生中睡眠时间在此范围内的人数是多少？

    查看答案和解析>>

    某校课外活动小组为了解本校九年级学生的睡眠时间情况，对学校若干名九年级学生的睡眠时间进行了抽查，将所得数据整理后，画出了频数分布直方图的一部分，如图，已知图中从左至右前5个小组的频率分别是0.04，0.08，0.24，0.28，0.24，第二小组的频数为4．

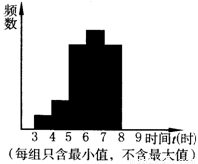
    请回答下列问题：

    （1）这次被抽查的学生人数是多少？并请补全频数分布直方图．

    （2）被抽查的学生中，睡眠时间在哪个范围内的人数最多？这一范围内的人数是多少？

    （3）如果该学校有900名九年级学生，若合理睡眠时间范围为7≤t<9，那么请你估计一下这个学校九年级学生中睡眠时间在此范围内的人数是多少？

     

    查看答案和解析>>

     （2011山东青岛，11，3分）某车间加工120个零件后，采用了新工艺.工效是原来的1.5倍，这样加工同样多的零件就少用1小时.采用新工艺前每小时加工多少个零件？若设采用新工艺前每小时加工x个零件，则根据题意可列方程为        .

     

    查看答案和解析>>


    同步练习册答案