
题目列表(包括答案和解析)
| 1 | 2 |
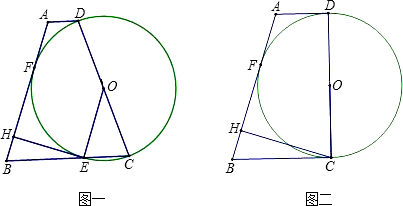
 (1997•吉林)作图题:
(1997•吉林)作图题:(2011吉林长春,6,3分)小玲每天骑自行车或步行上学,她上学的路程为![]() 米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为
米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为![]() 米/分.根据题意,下面列出的方程正确的是
米/分.根据题意,下面列出的方程正确的是
(A)![]() . (B)
. (B)![]() .
.
(C)![]() . (D)
. (D)![]() .
.
(2011吉林长春,6,3分)小玲每天骑自行车或步行上学,她上学的路程为 米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为
米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为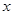 米/分.根据题意,下面列出的方程正确的是
米/分.根据题意,下面列出的方程正确的是
(A) . (B)
. (B)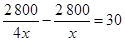 .
.
(C) . (D)
. (D)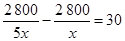 .
.
 米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为
米,骑自行车的平均速度是步行平均速度的4倍,骑自行车比步行上学早到30分钟.设小玲步行的平均速度为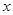 米/分.根据题意,下面列出的方程正确的是
米/分.根据题意,下面列出的方程正确的是A. . . | B. . . |
C.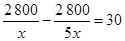 . . | D. . . |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com