
题目列表(包括答案和解析)
给出下列5个命题:
①![]() 是函数
是函数![]() 在区间(
在区间(![]() ,4]上为单调减函数的充要条件;
,4]上为单调减函数的充要条件;
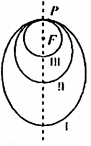 ②如图所示,“嫦娥探月卫星”沿地月转移轨道飞向月球,在月球附近一点P进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2Cl和2c2分别表示摘圆轨道I和II的焦距,用2a1和2a2分别表示椭圆轨道I和II的长轴的长,则有
②如图所示,“嫦娥探月卫星”沿地月转移轨道飞向月球,在月球附近一点P进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2Cl和2c2分别表示摘圆轨道I和II的焦距,用2a1和2a2分别表示椭圆轨道I和II的长轴的长,则有![]() ;
;
③函数![]() 与它的反函数
与它的反函数![]() 的图象若相交,则交点必在直线y =x上;
的图象若相交,则交点必在直线y =x上;
④己知函数![]() 在(O, 1)上满足,
在(O, 1)上满足,![]() ,贝U
,贝U![]() ;
;
⑤函数.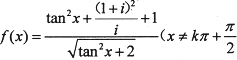 ,
,![]() ,/为虚数单位)的最小值为2
,/为虚数单位)的最小值为2
其中所有真命题的代号是_____________________
给出下列5个命题:
 ①
①![]() 是函数
是函数![]() 在区间(
在区间(![]() ,4]上为单调减函数的充要条件;
,4]上为单调减函数的充要条件;
②如图所示,“嫦娥探月卫星”沿地月转移轨道飞向月球,在月球附近一点P进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2Cl和2c2分别表示摘圆轨道I和II的焦距,用2a1和2a2分别表示椭圆轨道I和II的长轴的长,则有![]() ;
;
③函数![]() 与它的反函数
与它的反函数![]() 的图象若相交,则交点必在直线y =x上;
的图象若相交,则交点必在直线y =x上;
④己知函数![]() 在(O, 1)上满足,
在(O, 1)上满足,![]() ,贝U
,贝U![]() ;
;
⑤函数.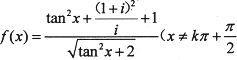 ,
,![]() ,/为虚数单位)的最小值为2
,/为虚数单位)的最小值为2
其中所有真命题的代号是_____________________高考高考资源
给出下列5个命题:
①![]() 是函数
是函数![]() 在区间(
在区间(![]() ,4]上为单调减函数的充要条件;
,4]上为单调减函数的充要条件;
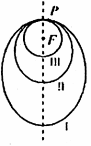
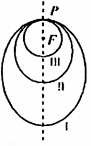 ②如图所示,“嫦娥探月卫星”沿地月转移轨道飞向月球,在月球附近一点P进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2Cl和2c2分别表示摘圆轨道I和II的焦距,用2a1和2a2分别表示椭圆轨道I和II的长轴的长,则有
②如图所示,“嫦娥探月卫星”沿地月转移轨道飞向月球,在月球附近一点P进入以月球球心F为一个焦点的椭圆轨道I绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道II绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道III绕月飞行,若用2Cl和2c2分别表示摘圆轨道I和II的焦距,用2a1和2a2分别表示椭圆轨道I和II的长轴的长,则有![]() ;
;
③函数![]() 与它的反函数
与它的反函数![]() 的图象若相交,则交点必在直线y =x上;
的图象若相交,则交点必在直线y =x上;
④己知函数![]() 在(O, 1)上满足,
在(O, 1)上满足,![]() ,贝U
,贝U![]() ;
;
⑤函数.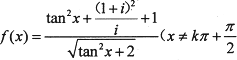 ,
,![]() ,/为虚数单位)的最小值为2
,/为虚数单位)的最小值为2
其中所有真命题的代号是_____________________
| 3 |
| 3 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com