
题目列表(包括答案和解析)
如何理解对数的概念及性质?
| OP |
| OQ |
| GD |
| GC |
| GE |
| GA |
| GF |
| GB |
| 1 |
| 2 |
(本小题考查函数定义域的概念及综合知识的应用 )
函数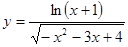 的定义域为
的定义域为
A.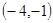 B
B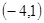 C
C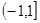 D
D 。
。
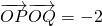 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.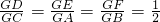 .
.A.
【命题意图】本题考查复数的概念及运算,容易题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com