
题目列表(包括答案和解析)
如图所示,在棱长为![]() 的正方体ABCD—A1B1C1D1中,E、F、H分
的正方体ABCD—A1B1C1D1中,E、F、H分
|
(1)求证:BH//平面A1EFD1;
(2)求直线AF与平面A1EFD1所成的角的正弦值。
21.(本题15分)已知函数![]() ,
,
![]() 在x=1处的切线的斜率为-1,
在x=1处的切线的斜率为-1,
(1)求![]() 的解析式及单调区间;
的解析式及单调区间;
(2)是否总存在实数m,使得对任意的![]() ,总存在
,总存在![]() ,使得
,使得
![]() 成立?若存在,求出实数m的取值范围;若不存在,说明理由.
成立?若存在,求出实数m的取值范围;若不存在,说明理由.
运用函数
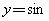 x,x∈[0,
x,x∈[0, )的图像及正弦定理,说明平面几何中的定理“在三角形中,较大的边所对的角也较大,较小的边所对的角也较小”的正确性.
)的图像及正弦定理,说明平面几何中的定理“在三角形中,较大的边所对的角也较大,较小的边所对的角也较小”的正确性.已知向量 =(
=( ),
), =(
=(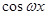 ,
,
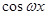 ),其中(
),其中(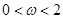 ).函数
).函数 ,其图象的一条对称轴为
,其图象的一条对称轴为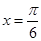 .
.
(I)求函数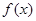 的表达式及单调递增区间;
的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若 =1,b=l,S△ABC=
=1,b=l,S△ABC=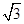 ,求a的值.
,求a的值.
【解析】第一问利用向量的数量积公式表示出
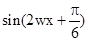 ,然后利用
,然后利用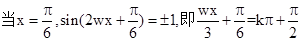 得到
得到 ,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
解:因为

由余弦定理得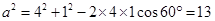 ,……11分故
,……11分故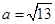
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com