
题目列表(包括答案和解析)
| σ | 2 |
| 1 |
| N |
| 1 |
| N |
角的产生来源于人们在日常生活中对于几何图形的观察(如支架、房顶等形成的图形)而产生.角的发展同样源于生产、生活的需要.初中我们学习过锐角、直角、钝角、周角等概念.请同学们思考下面的角度如何表示.
1.你的手表慢了5分钟,想将它校准,分针应该旋转多少度?
2.假如你的手表快了2.5小时,想将它校准,分针旋转多少度?
材料:在高一物理学习中,我们学习过力的分解,一个力可以分解为平面内任意两个方向上的力.如下图,
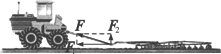
拖拉机拉着耙,对耙的拉力是斜向上方的,我们可以说,这个力产生两个效果:使耙克服泥土的阻力前进,同时把耙向上提,使它不会插得太深.这两个效果相当于两个力分别产生的:一个水平的力F1使耙前进,一个竖直向上的力F2把耙上提,即力F可以用两个力F1和F2来代替,即力F被分解成两个力F1和F2.
利用你所学知识,能不能将上面的物理知识抽象为数学知识?这一数学知识有何作用?
在统计学中,我们学习过方差的概念,其计算公式为![]() ,
,
并且知道,其中![]() 为x1、x2、…、xn的平均值.
为x1、x2、…、xn的平均值.
类似地,现定义“绝对差”的概念如下:设有n个实数x1、x2、…、xn,称函数g(x)=|x-x1|+|x-x2|+…+|x-xn|为此n个实数的绝对差.
(1)设有函数g(x)=|x+1|+|x-1|+|x-2|,试问当x为何值时,函数g(x)取到最小值,并求最小值;
(2)设有函数g(x)=|x-x1|+|x-x2|+…+|x+x2|,(x∈R,x1<x2<…<xn∈R),
试问:当x为何值时,函数g(x)取到最小值,并求最小值;
(3)若对各项绝对值前的系数进行变化,试求函数f(x)=3|x+3|+2|x-1|-4|x-5|(x∈R)的最值;
(4)受(3)的启发,试对(2)作一个推广,给出“加权绝对差”的定义,并讨论该函数的最值(写出结果即可).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com