练习册

  • 练习册
  • 试题
    8． 如图.在长方体ABCD-A1B1C1D1中.已知AB=4.AD=3.AA1=2.E.F分别是线段AB.BC上的点.且EB=BF=1.求直线EC1与FD1所成的角的余弦值. 解:延长BA至点E1,使AE1=1,连结E1F.DE1.D1E1.DF.有D1C1//E1E, D1C1=E1E,则四边形D1E1EC1是平行四边形.则E1D1//EC1.于是∠E1D1F为直线与所成的角. 在Rt△BE1F中.. . 在Rt△D1DE1中, 在Rt△D1DF中, 在△E1FD1中,由余弦定理得: ∴直线与所成的角的余弦值为. 【查看更多】

     

    题目列表(包括答案和解析)

    (2004广东，13)某班委会由4名男生与3名女生组成，现从中选出2人担任正副班长，其中至少有1名女生当选的概率是_________(用分数作答)．

    查看答案和解析>>

    (2004广东，11)若，则

    [　　]

    A．f(0)＞f(－1)＞f(1)

    B．f(0)＞f(1)＞f(－1)

    C．f(1)＞f(0)＞f(－1)

    D．f(－1)＞f(0)＞f(1)

    查看答案和解析>>

    (2004广东，9)当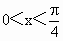时，函数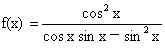的最小值是

    [　　]

    A．

    B．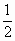

    C．2

    D．4

    查看答案和解析>>

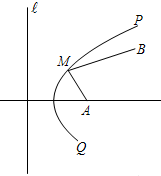    （2004•虹口区一模）如图，南北向的公路?，A地在公路的正东2km处，B地在A地北偏东30°方向4km处，河流沿岸PQ （曲线）上任一点到公路?及到A地距离均相等，现要在曲线PQ上选一处M建一座码头，向A、B两处转运货物，经测算从M到A，M到B修建公路的费用均为a 万元/km，那么修建这两条公路的总费用最低是（　　）

    查看答案和解析>>

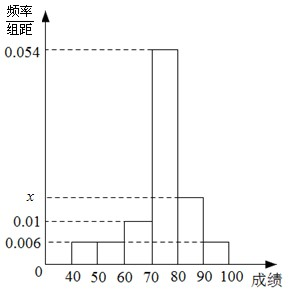    （2012•广东）某班50位学生期中考试数学成绩的频率直方分布图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
    （1）求图中x的值；
    （2）从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上（含90分）的人数记为ξ，求ξ的数学期望．

    查看答案和解析>>


    同步练习册答案