
题目列表(包括答案和解析)
利用定积分的定义计算![]() 的值.
的值.
设A是由m×n个实数组成的m行n列的数表,满足:每个数的绝对值不大于1,且所有数的和为零,记s(m,n)为所有这样的数表构成的集合。
对于A∈S(m,n),记ri(A)为A的第ⅰ行各数之和(1≤ⅰ≤m),Cj(A)为A的第j列各数之和(1≤j≤n):
记K(A)为∣r1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。
(1) 对如下数表A,求K(A)的值;
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A∈S(2,3)形如
|
1 |
1 |
c |
|
a |
b |
-1 |
求K(A)的最大值;
(3)给定正整数t,对于所有的A∈S(2,2t+1),求K(A)的最大值。
【解析】(1)因为 ,
,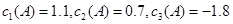
所以
(2) 不妨设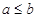 .由题意得
.由题意得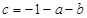 .又因为
.又因为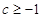 ,所以
,所以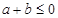 ,
,
于是 ,
,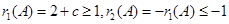 ,
,
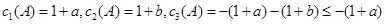
所以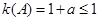 ,当
,当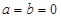 ,且
,且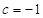 时,
时,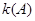 取得最大值1。
取得最大值1。
(3)对于给定的正整数t,任给数表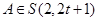 如下,
如下,
|
|
|
… |
|
|
|
|
… |
|
任意改变A的行次序或列次序,或把A中的每一个数换成它的相反数,所得数表
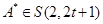 ,并且
,并且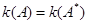 ,因此,不妨设
,因此,不妨设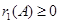 ,
,
且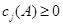
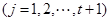 。
。
由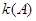 得定义知,
得定义知,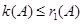 ,
,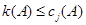
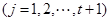
又因为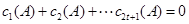
所以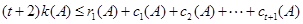
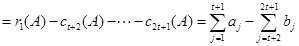
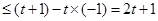
所以,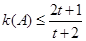
对数表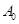 :
:
|
1 |
1 |
… |
1 |
|
… |
|
|
|
|
… |
|
-1 |
… |
-1 |
则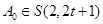 且
且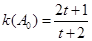 ,
,
综上,对于所有的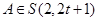 ,
,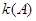 的最大值为
的最大值为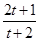
复数的模
(1)向量![]() 的模r,叫做复数Z=a+bi的_________,记作|Z|或|a+bi|.如果b=0,那么Z=a+bi是一个实数a,它的模等于|a|(也就是a的绝对值).由模的定义知|Z|=|a+bi|=r=_________.(r≥0,r∈R)
的模r,叫做复数Z=a+bi的_________,记作|Z|或|a+bi|.如果b=0,那么Z=a+bi是一个实数a,它的模等于|a|(也就是a的绝对值).由模的定义知|Z|=|a+bi|=r=_________.(r≥0,r∈R)
(2)为方便起见,我们常把复数Z=a+bi说成点Z或说成向量![]() ,并且规定,相等的向量表示_________.
,并且规定,相等的向量表示_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com