
题目列表(包括答案和解析)
| n2+n |
| 12+1 |
| k2+k |
| (k+1)2+(k+1) |
| k2+3k+2 |
| (k2+3k+2)+(k+2) |
| (k+2)2 |
| A、过程全部正确 |
| B、n=1验得不正确 |
| C、归纳假设不正确 |
| D、从n=k到n=k+1的推理不正确 |
对于不等式![]() <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下:
(1)当n=1时,![]() <1+1,不等式成立.
<1+1,不等式成立.
(2)假设当n=k(k∈N*且k≥1)时,不等式成立,即![]() <k+1,则当n=k+1时,
<k+1,则当n=k+1时,![]() =
=![]() <
<![]() =
=![]() =(k+1)+1,
=(k+1)+1,
所以当n=k+1时,不等式成立,则上述证法 ( ).
A.过程全部正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
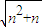 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: <1+1,不等式成立.
<1+1,不等式成立. <k+1,则当n=k+1时,
<k+1,则当n=k+1时,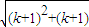 =
=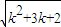 <
< =
= =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.已知数列 满足:
满足: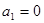 ,
,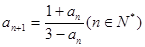
(Ⅰ)计算 的值;
的值;
(Ⅱ)由(Ⅰ)的结果猜想 的通项公式,并用数学归纳法证明你的结论.
的通项公式,并用数学归纳法证明你的结论.
【解析】本试题主要考查了数列的通项公式的求解和猜想和数学归纳法的证明。
 <n+1(n∈N*),某同学用数学归纳法的证明过程如下:
<n+1(n∈N*),某同学用数学归纳法的证明过程如下: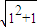 <1+1,不等式成立.
<1+1,不等式成立. <k+1,则当n=k+1时,
<k+1,则当n=k+1时, =
= <
< =
= =(k+1)+1,∴当n=k+1时,不等式成立.
=(k+1)+1,∴当n=k+1时,不等式成立.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com