
题目列表(包括答案和解析)
 I、下列说法正确的是
I、下列说法正确的是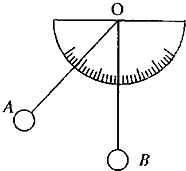 (2011?唐山二模)如图所示,把A、B两个小球用等长细线悬挂起来,一小球自然下垂,拉起另一个小球,放下时它们将相碰,请你利用该实验方法验证动量守恒定律.
(2011?唐山二模)如图所示,把A、B两个小球用等长细线悬挂起来,一小球自然下垂,拉起另一个小球,放下时它们将相碰,请你利用该实验方法验证动量守恒定律.| (1-cosα) |
| (1-cosγ) |
| (1-cosβ) |
| (1-cosα) |
| (1-cosγ) |
| (1-cosβ) |
选做题(请从A、B和C三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答,则按A、B两小题评分.)
A.(选修模块3-3)(12分)
(1) (4分)下列说法中正确的是
A.当两个分子间的距离为r0(平衡位置)时,分子力为零,分子势能最小
B.扩散现象和布朗运动的剧烈程度都与温度有关,所以扩散现象和布朗运动也叫做热运动
C.第二类永动机不违反能量守恒定律,但违反了热力学第二定律
D.自然界中与热现象有关的自发的能量转化过程具有方向性,虽然总能量守恒,但能量品质在退化
(2)(4分)如图所示,在开口向上的竖直放置圆筒形容器内用质量为m活塞密 封一部分气体,活塞与容器壁间能无摩擦滑动,大气压恒为p0,容器的横截面积为S,密封气体的压强是 ,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,在此过程中密闭气体的内能增加 。
封一部分气体,活塞与容器壁间能无摩擦滑动,大气压恒为p0,容器的横截面积为S,密封气体的压强是 ,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,在此过程中密闭气体的内能增加 。
(3)晶须是一种发展中的高强度材料,它是一些非常细的完整的丝状(横截面为圆形)晶体.现有一根铁(Fe)晶,直径为d,能承受的最大拉力为F.试求刚要拉断时原子间的作用力f.(已知铁的密度ρ,铁的摩尔质量M,阿伏伽德罗常数为NA,忽略铁分子间的空隙)
B.(选修模块3-4)(12分)
(l)(4分)下列有关光现象的说法中正确的是
A.同种介质中,光波长越短,传播速度越快
B.薄膜干涉条纹可以看着是等厚线
C.眼睛直接观察全息照片可以看到立体图象
D.宇航员驾驶一艘接近光速的宇宙飞船飞行时,他不能感知自身质量的增大
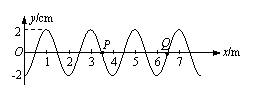 (2)(4分)沿x轴正方向传播的简谐横波在t=0时的波形如图所示,P、Q两个质点的平衡位置分别位于x=3.5m和x=6.5m处。在t1=0.5s时,质点P此后恰好第二次处于波峰位置;则t2= s时,质点Q此后第二次在平衡位置且向上运动;当t3=0.9s时,质点P的位移为__ ____cm。
(2)(4分)沿x轴正方向传播的简谐横波在t=0时的波形如图所示,P、Q两个质点的平衡位置分别位于x=3.5m和x=6.5m处。在t1=0.5s时,质点P此后恰好第二次处于波峰位置;则t2= s时,质点Q此后第二次在平衡位置且向上运动;当t3=0.9s时,质点P的位移为__ ____cm。
 (3)(4分) 如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质的C点,DC与AB的距离H=
(3)(4分) 如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质的C点,DC与AB的距离H=![]() R/2,若DC光线进入介质球后经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,求介质的折射率。
R/2,若DC光线进入介质球后经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,求介质的折射率。
C.(选修模块3-5)(12分)
(1)(4分)下列说法正确的是
A.任何一种金属都存在一个“最大波长”,入射光波长小于这个波长,才能产生光电效应
B.氢原子辐射出一个光子后能量减小,核外电子的运动加速度减小
C.用电子流工作的显微镜比用相同速度的质子流工作的显微镜分辨率低
D.核力的饱和性决定了原子核太大,那一定是不稳定的
(2)(4分)质量为m1的锂核(![]() )俘获一个质量为m2的质子后衰变为两个
)俘获一个质量为m2的质子后衰变为两个![]() 粒子,
粒子,![]() 粒子质量为m3,已知光在真空中速度为c.
粒子质量为m3,已知光在真空中速度为c.
①写出核反应方程 。
②该过程中释放的核能为ΔE =
(3) (4分)在![]() 粒子散射实验中,质量为m的
粒子散射实验中,质量为m的![]() 粒子以初动能E0与质量M的金核发生对心碰撞。若金核初时静止且自由,求
粒子以初动能E0与质量M的金核发生对心碰撞。若金核初时静止且自由,求![]() 粒子与金核间距离最近时电势能。
粒子与金核间距离最近时电势能。
选做题(请从A、B和C三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答,则按A、B两小题评分.)
A.(选修模块3-3)(12分)
(1) (4分)下列说法中正确的是
A.当两个分子间的距离为r0(平衡位置)时,分子力为零,分子势能最小
B.扩散现象和布朗运动的剧烈程度都与温度有关,所以扩散现象和布朗运动也叫做热运动
C.第二类永动机不违反能量守恒定律,但违反了热力学第二定律
D.自然界中与热现象有关的自发的能量转化过程具有方向性,虽然总能量守恒,但能量品质在退化
(2)(4分)如图所示,在开口向上的竖直放置圆筒形容器内用质量为m活塞密 封一部分气体,活塞与容器壁间能无摩擦滑动,大气压恒为p0,容器的横截面积为S,密封气体的压强是 ,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,在此过程中密闭气体的内能增加 。
封一部分气体,活塞与容器壁间能无摩擦滑动,大气压恒为p0,容器的横截面积为S,密封气体的压强是 ,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,在此过程中密闭气体的内能增加 。
(3)晶须是一种发展中的高强度材料,它是一些非常细的完整的丝状(横截面为圆形)晶体.现有一根铁(Fe)晶,直径为d,能承受的最大拉力为F.试求刚要拉断时原子间的作用力f.(已知铁的密度ρ,铁的摩尔质量M,阿伏伽德罗常数为NA,忽略铁分子间的空隙)
B.(选修模块3-4)(12分)
(l)(4分)下列有关光现象的说法中正确的是
A.同种介质中,光波长越短,传播速度越快
B.薄膜干涉条纹可以看着是等厚线
C.眼睛直接观察全息照片可以看到立体图象
D.宇航员驾驶一艘接近光速的宇宙飞船飞行时,他不能感知自身质量的增大
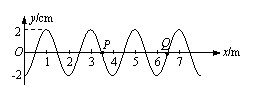 (2)(4分)沿x轴正方向传播的简谐横波在t=0时的波形如图所示,P、Q两个质点的平衡位置分别位于x=3.5m和x=6.5m处。在t1=0.5s时,质点P此后恰好第二次处于波峰位置;则t2=
s时,质点Q此后第二次在平衡位置且向上运动;当t3=0.9s时,质点P的位移为__ ____cm。
(2)(4分)沿x轴正方向传播的简谐横波在t=0时的波形如图所示,P、Q两个质点的平衡位置分别位于x=3.5m和x=6.5m处。在t1=0.5s时,质点P此后恰好第二次处于波峰位置;则t2=
s时,质点Q此后第二次在平衡位置且向上运动;当t3=0.9s时,质点P的位移为__ ____cm。
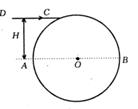 (3)(4分) 如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质的C点,DC与AB的距离H=
(3)(4分) 如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质的C点,DC与AB的距离H=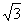 R/2,若DC光线进入介质球后经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,求介质的折射率。
R/2,若DC光线进入介质球后经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,求介质的折射率。
C.(选修模块3-5)(12分)
(1)(4分)下列说法正确的是
A.任何一种金属都存在一个“最大波长”,入射光波长小于这个波长,才能产生光电效应
B.氢原子辐射出一个光子后能量减小,核外电子的运动加速度减小
C.用电子流工作的显微镜比用相同速度的质子流工作的显微镜分辨率低
D.核力的饱和性决定了原子核太大,那一定是不稳定的
(2)(4分)质量为m1的锂核(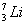 )俘获一个质量为m2的质子后衰变为两个
)俘获一个质量为m2的质子后衰变为两个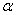 粒子,
粒子,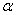 粒子质量为m3,已知光在真空中速度为c.
粒子质量为m3,已知光在真空中速度为c.
①写出核反应方程 。
②该过程中释放的核能为ΔE =
(3) (4分)在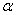 粒子散射实验中,质量为m的
粒子散射实验中,质量为m的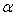 粒子以初动能E0与质量M的金核发生对心碰撞。若金核初时静止且自由,求
粒子以初动能E0与质量M的金核发生对心碰撞。若金核初时静止且自由,求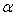 粒子与金核间距离最近时电势能。
粒子与金核间距离最近时电势能。
 ,其中v10和v20分别是碰撞前两物体
,其中v10和v20分别是碰撞前两物体

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com