
题目列表(包括答案和解析)
以下说法中正确的是
① 甲乙两同学各自独立地考察了两个变量 的线性相关关系时,发现两个人对
的线性相关关系时,发现两个人对 的观测数据的平均值相等,都是
的观测数据的平均值相等,都是 。对
。对 的观测数据的平均值也相等,都是
的观测数据的平均值也相等,都是 。各自求出的回归直线分别是
。各自求出的回归直线分别是 ,则直线
,则直线 必定相交于定点
必定相交于定点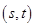 。
。
②用独立性检验(2×2列联表法)来考察两个分类变量 是否有关系时,算出的随机变量
是否有关系时,算出的随机变量 的值越大,说明“
的值越大,说明“ 有关系”成立的可能性越大。
有关系”成立的可能性越大。
③合情推理就是正确的推理。
④最小二乘法的原理是使得 最小。
最小。
⑤用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合程度越好。
越小,说明模型的拟合程度越好。
甲、乙两同学各自独立地考察两个变量 的线性相关关系时,发现两人对
的线性相关关系时,发现两人对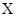 的观察数据的平均值相等,都是
的观察数据的平均值相等,都是 ,对
,对 的观察数据的平均值也相等,都是
的观察数据的平均值也相等,都是 ,各自求出的回归直线分别是
,各自求出的回归直线分别是 ,则直线与必过同一点____________
,则直线与必过同一点____________
商品零售商要了解每周的广告费及消费额(单位:万元)之间的关系,记录如下:
| 广告费(x) | 40 | 28 | 33 | 36 | 25 | 43 | 38 | 30 | 50 | 20 | 42 | 46 |
| 销售额(y) | 490 | 395 | 420 | 475 | 385 | 525 | 480 | 400 | 560 | 365 | 510 | 540 |
利用上述资料:
画出散点图;
求销售额y对广告费x的一元线性回归方程;
求出两个变量的相关系数。
|
广告费x |
40 |
28 |
33 |
36 |
25 |
43 |
38 |
30 |
50 |
20 |
42 |
46 |
|
销售额y |
490 |
395 |
420 |
475 |
385 |
525 |
480 |
400 |
560 |
365 |
510 |
540 |
利用上述资料:
(1)画出散点图;
(2)求销售额y对广告费x的一元线性回归方程;
(3)求出两个变量的相关系数。
以下说法中正确的是 ![]()
① 甲乙两同学各自独立地考察了两个变量![]() 的线性相关关系时,发现两个人对
的线性相关关系时,发现两个人对![]() 的观测数据的平均值相等,都是
的观测数据的平均值相等,都是![]() 。对
。对![]() 的观测数据的平均值也相等
的观测数据的平均值也相等![]() ,都是
,都是![]() 。各自求出
。各自求出![]() 的回归直线分别是
的回归直线分别是![]() ,则直线
,则直线![]() 必定相交于定点
必定相交于定点![]() 。
。
②用独立性检验(2×2列联表法)来考察两个分类变量![]() 是否有关系时,算出的随机变量
是否有关系时,算出的随机变量![]() 的值越大,说明“
的值越大,说明“![]() 有关系”成立的可能性越大。
有关系”成立的可能性越大。
③合情推理就是正确的推理。
④最小二乘法的原理是使得![]() 最小。
最小。
⑤用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型的拟合程度越好。
越小,说明模型的拟合程度越好。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com