
题目列表(包括答案和解析)
![]()
b)∈M,且对M中的其它元素(c,d),总有c≥a,则a=____.
![]() b)∈M,且对M中的其它元素(c,d),总有c≥a,则a=____.
b)∈M,且对M中的其它元素(c,d),总有c≥a,则a=____.
分析:读懂并能揭示问题中的数学实质,将是解决该问题的突破口.怎样理解“对M中的其它元素(c,d),总有c≥a”?M中的元素又有什么特点?
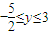 },若(a,b)∈M,且对M中的其它元素(c,d),总有c≥a,则a= .
},若(a,b)∈M,且对M中的其它元素(c,d),总有c≥a,则a= .| 5 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com