（2005•普陀区一模）人口问题其实是许多国家的政府都要面对的问题．05年10月24日出版的《环球时报》就报道了一篇俄罗斯政府目前遭遇“人口危机”的文章．报道中引用了以下来自俄政府公布的数据：
●截至05年6月底，俄罗斯人口为1.431亿，人口密度每平方公里只有8.38人；
●04年一年俄人口就减少了76万，05年1月至5月共又减少了35.9万；
●据俄联邦安全会议预测，到2050年，俄将只有约1亿人口，比目前锐减30%．
试根据以上数据信息回答下列问题：
（1）以04年至05年5月这17个月平均每月人口减少的数据为基础，假设每月人口减少相同，预测到2050年6月底，俄罗斯的人口约为多少亿？（保留三位小数）
（2）按第（1）小题给定的预测方法，到何时俄罗斯的人口密度将低于每平方公里5人？

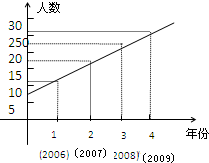某中学，由于不断深化教育改革，办学质量逐年提高．2006年至2009年高考考入一流大学人数如下：

年       份	2006	2007	2008	2009
高考上线人数	116	172	220	260

以年份为横坐标，当年高考上线人数为纵坐标建立直角坐标系，由所给数据描点作图（如图所示），从图中可清楚地看到这些点基本上分布在一条直线附近，因此，用一次函数y=ax+b来模拟高考上线人数与年份的函数关系，并以此来预测2010年高考一本上线人数．如下表：

年     份	2006	2007	2008	2009
年份代码x	1	2	3	4
实际上线人数	116	172	220	260
模拟上线人数	y1=a+b	y2=2a+b	y3=3a+b	y4=4a+b

为使模拟更逼近原始数据，用下列方法来确定模拟函数．
设S=（y₁-y₁′）²+（y₂-y₂′）²+（y₃-y₃′）²+（y₄-y₄′）²，y₁′、y₂′、y₃′、y₄′表示各年实际上线人数，y₁、y₂、y₃、y₄表示模拟上线人数，当S最小时，模拟函数最为理想．试根据所给数据，预测2010年高考上线人数．