题目列表(包括答案和解析)
已知a＝(2cosx，cos2x)，b＝(sinx，－
)，f(x)＝a·b.
(1)求f(x)的振幅、周期，并画出它在一个周期内的图象；
(2)说明它可以由函数y＝sinx的图象经过怎样的变换得到．
)，f(x)＝a·b.已知a＝(2cosx，cos2x)，b＝(sinx，－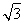
)，f(x)＝a·b.
(1)求f(x)的振幅、周期，并画出它在一个周期内的图象；
(2)说明它可以由函数y＝sinx的图象经过怎样的变换得到．
在等式cos2x＝2cos2x－1(x∈R)的两边求导，得：
，由求导法则，得(－sin2x)·2＝4cosx·(－sinx)，化简得等式：sin2x＝2cosx·sinx．
(1)利用上题的想法(或其他方法)，结合等式
(x∈R，正整数n≥2)，证明：
．
(2)对于正整数n≥3，求证：
(i)
；
(ii)
；
(iii)
．
设函数f(x)＝m·n，其中向量m＝(asin，x2b)，n＝(2cosx，cos2x)，(x∈R)，且f(0)＝f(
)＝2．
(1)求函数f(x)的解析式，并写出最小正周期及单调增区间；
(2)当x∈[－
]时，求函数f(x)的值域．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com