
题目列表(包括答案和解析)
16.
(本小题满分12分)已知函数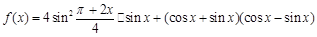 .
.
(1)
化简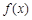 ;
;
(2)
已知常数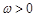 ,若函数
,若函数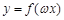 在区间
在区间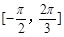 上是增函数,求
上是增函数,求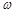 的取值范围;
的取值范围;
(3)
若方程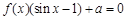 有解,求实数a的取值范围.[来源:]
有解,求实数a的取值范围.[来源:]
(1)
化简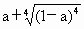 的结果是
的结果是
[
]A.1 B.2a-1 C.1或2a-1 D.0
(2)当a、bÎR时,下列各式总能成立的是
[
A.![]() B.
B.![]()
C.![]() D.
D.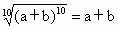
(1)化简 的结果是
的结果是
[ ]
(2)当a、bÎ R时,下列各式总能成立的是
[ ]




化简:
 为
为
[ ]
A.1 B.-1 C.-tan2α D.tan2α
已知f(x)=![]() +
+![]() ,并且x≠2kπ+
,并且x≠2kπ+![]() ,k∈Z;.
,k∈Z;.
(1)化简f(x);
(2)是否存在x,使得tan![]() ·f(x)与
·f(x)与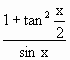 相等?若存在,求x的值;若不存在,请说明理由.
相等?若存在,求x的值;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com