
题目列表(包括答案和解析)
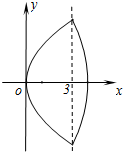 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 9y2 |
| 8 |
|
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| r1 |
| r2 |
(1)设椭圆 :
: 与双曲线
与双曲线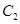 :
: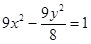 有相同的焦点
有相同的焦点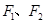 ,
,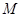 是椭圆
是椭圆 与双曲线
与双曲线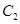 的公共点,且
的公共点,且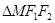 的周长为
的周长为 ,求椭圆
,求椭圆 的方程;
的方程;
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.
(2)如图,已知“盾圆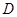 ”的方程为
”的方程为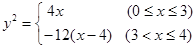 .设“盾圆
.设“盾圆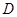 ”上的任意一点
”上的任意一点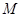 到
到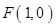 的距离为
的距离为 ,
,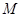 到直线
到直线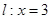 的距离为
的距离为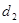 ,求证:
,求证: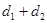 为定值;
为定值;

(3)由抛物线弧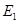 :
: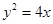 (
(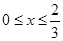 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧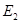 :
: (
(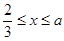 )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆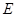 ”.设过点
”.设过点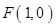 的直线与“盾圆
的直线与“盾圆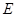 ”交于
”交于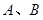 两点,
两点, ,
,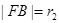 且
且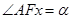 (
(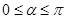 ),试用
),试用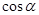 表示
表示 ;并求
;并求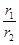 的取值范围.
的取值范围.
 (1)设椭圆C1:
(1)设椭圆C1: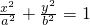 与双曲线C2:
与双曲线C2: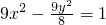 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;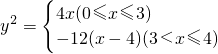 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 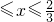 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: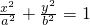 (
(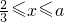 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求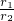 的取值范围.
的取值范围.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com