
题目列表(包括答案和解析)
(08年东北师大附中)(12分)
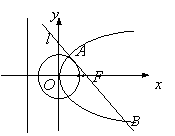
已知![]() 是抛物线
是抛物线![]() 的焦点,过
的焦点,过![]() 的直线
的直线![]() 与圆
与圆![]() :
:![]() 切于点
切于点![]()
![]() .
.
(Ⅰ) 求抛物线![]() 的方程;
的方程;
(Ⅱ) 若![]() 与抛物线交于
与抛物线交于![]() 两点,
两点,![]() 在直线
在直线![]() :
:![]() 上,
上,![]() 点在圆
点在圆![]() 上,求当
上,求当![]() 时,△
时,△![]() 面积的最大值.
面积的最大值.
(08年东北师大附中文)(12分)
已知等差数列![]() ,
,![]() ,公差
,公差![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
(08年东北师大附中) (10分) 在△![]() 中,角A、B、C的对边分别为a、b、c, △ABC的外接圆半径R =
中,角A、B、C的对边分别为a、b、c, △ABC的外接圆半径R =![]() ,且满足
,且满足![]() .
.
(Ⅰ)求角B和边b的大小;
(Ⅱ)求△![]() 的面积的最大值.
的面积的最大值.
(08年东北师大附中理)(12分)
某市举行的一次数学新课程骨干教师培训,共邀请10名使用不同版本教材的教师,数据如下表所示:
版本 | 人教A版 | 人教B版 | ||
性别 | 男教师 | 女教师 | 男教师 | 女教师 |
人数 | 3 | 2 | 2 | 3 |
(Ⅰ)从这10名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(Ⅱ)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(08年东北师大附中)(12分)
已知各项均为正数的数列![]() 中,
中,![]() ,
, ![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com