
题目列表(包括答案和解析)

| 实验序号 | 拉力F作用点据左侧细线悬挂点距离△s | 木杆受到向下的拉力F(牛) | 左侧细线受到木杆对它的拉力F1(牛) | 右侧细线受到木杆对它的拉力F2(牛) |
| 1 | 0.3 | 10.0 | 7.0 | 3.0 |
| 2 | 0.3 | 20.0 | 14.0 | 6.0 |
| 3 | 0.3 | 30.0 | 21.0 | 9.0 |
| 4 | 0.4 | 10.0 | 6.0 | 4.0 |
| 5 | 0.4 | 20.0 | 12.0 | 8.0 |
| 6 | 0.4 | 30.0 | 18.0 | 12.0 |
| 7 | 0.5 | 10.0 | 5.0 | 5.0 |
| 8 | 0.5 | 20.0 | 10.0 | 10.0 |
| 9 | 0.5 | 30.0 | 15.0 | 15.0 |
| 时间 t(s) |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 弹簧秤 的示数 F(N) |
10 | 11.5 | 11.0 | 10.5 | 10.0 | 10.0 | 10.0 | 10.0 | 9.5 | 9.0 | 8.5 | 10.0 |
| 时间 t(s) |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 弹簧秤 的示数 F(N) |
10 | 8.5 | 9.0 | 9.5 | 10.0 | 10.0 | 10.0 | 10.0 | 10.5 | 11.0 | 11.5 | 10.0 |
 (2008?顺义区一模)小芳要探究金属圆柱受到水的浮力与浸在水中深度的关系,实验装置如图所示,将高为6cm的金属圆柱体缓慢浸入水中(水足够深),在金属圆柱体接触容器底之前,记下金属体下表面所处的不同深度h和弹簧测力计相应的拉力示数F,实验数据如下表:
(2008?顺义区一模)小芳要探究金属圆柱受到水的浮力与浸在水中深度的关系,实验装置如图所示,将高为6cm的金属圆柱体缓慢浸入水中(水足够深),在金属圆柱体接触容器底之前,记下金属体下表面所处的不同深度h和弹簧测力计相应的拉力示数F,实验数据如下表:| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| h/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| F/N | 9.0 | 8.6 | 8.2 | 7.8 | 7.4 | 7.0 | 6.6 | 6.6 | 6.6 | 6.6 | 6.6 | 6.6 |
| 实验次数 | F1(N) | l1(cm) | F1?l1(N?cm) | F2(N) | l2(cm) | F2?l2(N?cm) |
| 1 | 0.98 | 5 | 4.9 4.9 |
0.49 0.49 |
10 | 4.9 4.9 |
| 2 | 1.96 | 30 | 58.8 58.8 |
2.94 | 20 20 |
58.8 58.8 |
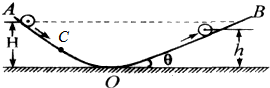 小敏想探究小球滚上斜面的最大高度与斜面倾角和小球质量的关系,将两个斜面AO与OB对接成如图装置,进行实验.
小敏想探究小球滚上斜面的最大高度与斜面倾角和小球质量的关系,将两个斜面AO与OB对接成如图装置,进行实验.| 实验 序号 |
小球质 量m/克 |
小球在斜面AO上 释放高度H/厘米 |
斜面OB 的倾角θ |
小球在斜面OB上 的最大高度h/厘米 |
| 1 | 5 | 10 | 40 | 9.0 |
| 2 | 30 | 8.6 | ||
| 3 | 20 | 8.0 | ||
| 4 | 7 | 10 | 40 | 9.0 |
| 5 | 30 | 8.6 | ||
| 6 | 20 | 8.0 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com