练习册

  • 练习册
  • 试题
    空间直角坐标系:如果空间的一个基底的三个基向量互相垂直.且长度都为1.则这个基底叫做单位正交基底.常用{i,j,k}表示.而空间坐标系的建立是:在空间选定一点O和一个单位正交基底{i,j,k}.以O为原点.分别以i,j,k的方向为正方向建立三条数轴:x轴.y轴.z轴.它们都叫坐标轴.O-xyz为空间坐标系.向量i,j,k为坐标向量.通过每两条数轴的平面叫做坐标平面.分别叫做xOy平面.yOz平面, xOz平面,作空间坐标系时.一般使∠xOy=135°.∠yOz=90°.在空间坐标系中.让右手拇指指向x轴的正方向.食指指向y轴的正方向.如果中指指向z轴的正方向.则称此坐标系为右手直角坐标系. 【查看更多】

     

    题目列表(包括答案和解析)

    （2009•闸北区二模）和平面解析几何的观点相同，在空间中，空间曲面可以看作是适合某种条件的动点的轨迹．一般来说，在空间直角坐标系O-xyz中，空间曲面的方程是一个三元方程F（x，y，z）=0．
    （Ⅰ）在直角坐标系O-xyz中，求到定点M0（0，2，-1）的距离为3的动点P的轨迹（球面）方程；
    （Ⅱ）如图，设空间有一定点F到一定平面α的距离为常数p＞0，即|FM|=2，定义曲面C为到定点F与到定平面α的距离相等（|PF|=|PN|）的动点P的轨迹，试建立适当的空间直角坐标系O-xyz，求曲面C的方程；  
    （Ⅲ）请类比平面解析几何中对二次曲线的研究，讨论曲面C的几何性质．并在图中通过画出曲面C与各坐标平面的交线（如果存在）或与坐标平面平行的平面的交线（如果必要）表示曲面C的大致图形．画交线时，请用虚线表示被曲面C自身遮挡部分．

    查看答案和解析>>

    一个四面体中如果有三条棱两两垂直，且垂足不是同一点，这三条棱就象中国武术中的兵器——三节棍，所以，我们常把这类四面体称为“三节棍体”， 三节棍体ABCD四个顶点在空间直角坐标系中的坐标分别为A（0,0,0）、B（0,4,0）、C（4,4,0）、D（0,0,2），则此三节棍体外接球的表面积是（    ）

    A.        B.        C.          D.

     

    查看答案和解析>>

    和平面解析几何的观点相同，在空间中，空间曲面可以看作是适合某种条件的动点的轨迹．一般来说，在空间直角坐标系O-xyz中，空间曲面的方程是一个三元方程F（x，y，z）=0．
    （Ⅰ）在直角坐标系O-xyz中，求到定点M（0，2，-1）的距离为3的动点P的轨迹（球面）方程；
    （Ⅱ）如图，设空间有一定点F到一定平面α的距离为常数p＞0，即|FM|=2，定义曲面C为到定点F与到定平面α的距离相等（|PF|=|PN|）的动点P的轨迹，试建立适当的空间直角坐标系O-xyz，求曲面C的方程；  
    （Ⅲ）请类比平面解析几何中对二次曲线的研究，讨论曲面C的几何性质．并在图中通过画出曲面C与各坐标平面的交线（如果存在）或与坐标平面平行的平面的交线（如果必要）表示曲面C的大致图形．画交线时，请用虚线表示被曲面C自身遮挡部分．

    查看答案和解析>>

    正四棱柱AC1中，底面ABCD是边长为4的正方形，A1C1与B1D1交于点N，BC1与B1C交于点M，且AM⊥BN，建立空间直角坐标系.

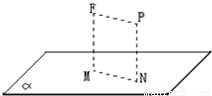
    （1）求AA1的长；

    （2）求〈,〉；

    （3）对于n个向量a1，a2，…,an，如果存在不全为零的n个实数λ1,λ2,…,λn，使得λ1a1+λ2a2+…+λ2an=0成立，则n个向量a1，a2，…，an叫做线性相关，不是线性相关的向量叫线性无关，判断、、是否线性相关，并说明理由.

    查看答案和解析>>


    同步练习册答案