
题目列表(包括答案和解析)
迭代法是用于求方程或方程组近似根的一种常用的算法设计方法.设方程为f(x)=0,用某种数学方法导出等价的形式x=g(x),然后按以下步骤执行:
(1)选一个方程的近似根,赋给变量x0;
(2)将x0的值保存于变量x1,然后计算g(x1),并将结果存于变量x0;
(3)当x0与x1的差的绝对值还不小于指定的精度要求时,重复步骤(2)的计算.
若方程有根,则按上述方法求得的x0就认为是方程的根.试用迭代法求某个数的平方根,用流程图和伪代码表示问题的算法.
已知函数f(x)=mx3+nx2(m、n∈R ,m≠0)的图像在(2,f(2))处的切线与x轴平行.
(1)求n,m的关系式并求f(x)的单调减区间;
(2)证明:对任意实数0<x1<x2<1, 关于x的方程:
![]() 在(x1,x2)恒有实数解
在(x1,x2)恒有实数解
(3)结合(2)的结论,其实我们有拉格朗日中值定理:若函数f(x)是在闭区间[a,b]上连续不断的函数,且在区间(a,b)内导数都存在,则在(a,b)内至少存在一点x0,使得![]() .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
当0<a<b时,![]() (可不用证明函数的连续性和可导性)
(可不用证明函数的连续性和可导性)
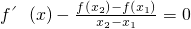 在(x1,x2)恒有实数解
在(x1,x2)恒有实数解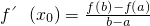 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明: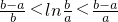 (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性). 在(x1,x2)恒有实数解
在(x1,x2)恒有实数解 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明: (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).厦门某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为错误!不能通过编辑域代码创建对象。(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为错误!不能通过编辑域代码创建对象。平方米,且高度不低于错误!不能通过编辑域代码创建对象。米.记防洪堤横断面的腰长为错误!不能通过编辑域代码创建对象。(米),外周长(梯形的上底线段错误!不能通过编辑域代码创建对象。与两腰长的和)为错误!不能通过编辑域代码创建对象。(米).
⑴求错误!不能通过编辑域代码创建对象。关于错误!不能通过编辑域代码创建对象。的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过错误!不能通过编辑域代码创建对象。米,则其腰长错误!不能通过编辑域代码创建对象。应在什么范围内?
⑶当防洪堤的腰长错误!不能通过编辑域代码创建对象。为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com