5．古典概型 (1)古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个,2)每个基本事件出现的可能性相等, (2)古典概型的概率计算公式:P(A)=, 一次试验连同其中可能出现的每一——青夏教育精英家教网—

5．古典概型 (1)古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个,2)每个基本事件出现的可能性相等, (2)古典概型的概率计算公式:P(A)=, 一次试验连同其中可能出现的每一个结果称为一个基本事件,通常此试验中的某一事件A由几个基本事件组成.如果一次试验中可能出现的结果有n个,即此试验由n个基本事件组成,而且所有结果出现的可能性都相等,那么每一基本事件的概率都是.如果某个事件A包含的结果有m个,那么事件A的概率P(A)=. 【查看更多】

题目列表(包括答案和解析)

在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球，现从甲、乙两个盒子中各取出1个球，每个小球被取出的可能性相等。

（1）求取出的两个球上标号为相邻整数的概率；

（2）求取出的两个球上标号之和能被3整除的概率.

【解析】本试题主要考查了古典概型概率的求解。第一问中，基本事件数为共有（1，1），（1，2），（1，3），（1，4），（2，1），（2，2），（2，3），（2，4），

（3，1），（3，2），（3，3），（3，4），（4，1），（4，2），（4，3），（4，4）

总数为16种．其中取出的两个小球上标号为相邻整数的基本事件有：

（1，2），（2，1），（2，3），（3，2），（3，4），（4，3）共6种利用古典概型可知，P=3 /8 ；

（2）其中取出的两个小球上标号之和能被3整除的基本事件有：

（1，2），（2，1），（2，4），（3，3），（4，2）共5种可得概率值5 /16 ；

解：甲、乙两个盒子里各取出1个小球计为（X，Y）则基本事件

共有（1，1），（1，2），（1，3），（1，4），（2，1），（2，2），（2，3），（2，4），

（3，1），（3，2），（3，3），（3，4），（4，1），（4，2），（4，3），（4，4）

总数为16种．

（1）其中取出的两个小球上标号为相邻整数的基本事件有：

（1，2），（2，1），（2，3），（3，2），（3，4），（4，3）共6种

故取出的两个小球上标号为相邻整数的概率P=3 /8 ；

（2）其中取出的两个小球上标号之和能被3整除的基本事件有：

（1，2），（2，1），（2，4），（3，3），（4，2）共5种

故取出的两个小球上标号之和能被3整除的概率为5 /16 ；

查看答案和解析>>

一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4．

（I）从袋中随机抽取一个球，将其编号记为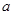，然后从袋中余下的三个球中再随机抽取一个球，将其编号记为．求关于的一元二次方程有实根的概率；

（II）先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n．若以作为点P的坐标，求点P落在区域内的概率．

【解析】第一问利用古典概型概率求解所有的基本事件数共12种，然后利用方程有实根，则满足△=4a²-4b²≥0，即a²≥b²。，这样求得事件发生的基本事件数为6种，从而得到概率。第二问中，利用所有的基本事件数为16种。即基本事件（m，n）有：（1，1）（1,2）（1,3）（1,4）（2,1）（2，2）（2,3）（2,4）（3,1）（3,2）（3，3）（3,4）（4,1）（4,2）（4,3）（4，4）共16种。在求解满足的基本事件数为（1，1）（2,1）（2，2）（3,1）共4种，结合古典概型求解得到概率。