2006年普通高等学校招生全国统一考试(北京卷) 理科综合能力测试试题卷(生物部分) 1.以下不能说明细胞全能性的实验是 A.胡萝卜韧皮部细胞培育出植株 B.紫色糯性玉米种子培育出植株 C.转入抗虫基因的棉花细胞培育出植株 D.番茄与马铃薯体细胞杂交后培育出植株 2.夏季,在晴天、阴天、多云、高温干旱四种天气条件下,猕猴桃的净光合作用强度(实际光合速率与呼吸速率之差)变化曲线不同,表示晴天的曲线图是 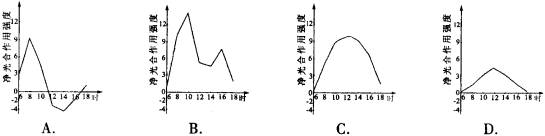
3.用蔗糖、奶粉和经蛋白酶水解后的玉米胚芽液,通过乳酸菌发酵可生产新型酸奶,下列相关叙述错误的是 A.蔗糖消耗量与乳酸生成量呈正相关 B.酸奶出现明显气泡说明有杂菌污染 C.应选择处于对数期的乳酸菌接种 D.只有奶粉为乳酸菌发酵提供氮源 4.用32P标记了玉米体细胞(含20条染色体)的DNA分子双链,再将这些细胞转入不含32P的培养基中培养,在第二次细胞分裂的中期、后期,一个细胞中的染色体总条数和被32P标记的染色体条数分别是 A.中期20和20、后期40和20 B.中期20和10、后期40和20 C.中期20和20、后期40和10 D.中期20和10、后期40和10 29.(12分)为合理利用水域资源,某调查小组对一个开放性水库生态系统进行了初步调查,部分数据如下表: 
(1)浮游藻类属于该生态系统成分中的 ,它处于生态系统营养结构中的 。 (2)浮游藻类数量少,能从一个方面反映水质状况好。调查数据分析表明:该水体具有一定的 能力。 (3)浮游藻类所需的矿质营养可来自细菌、真菌等生物的 ,生活在水库淤泥中的细菌代谢类型主要为 。 (4)该水库对游人开放一段时间后,检测发现水体己被氮、磷污染。为确定污染源是否来自游人,应检测 处浮游藻类的种类和数量。 30.(18分)为丰富植物育种的种质资源材料,利用钴60的γ射线辐射植物种子,筛选出不同性状的突变植株。请回答下列问题: (1)钴60的γ辐射用于育种的方法属于 育种。 (2)从突变材料中选出高产植株,为培育高产、优质、抗盐新品种,利用该植株进行的部分杂交实验如下: 
①控制高产、优质性状的基因位于 对染色体上,在减数分裂联会期 (能、不能)配对。 ②抗盐性状属于 遗传。 (3)从突变植株中还获得了显性高蛋白植株(纯合子)。为验证该性状是否由一对基因控制,请参与实验设计并完善实验方案: ①步骤1:选择 和 杂交。 预期结果: 。 ②步骤2: 。 预期结果: 。 ③观察实验结果,进行统计分析:如果 与 相符,可证明该性状由一对基因控制。 31.(18分)为研究长跑中运动员体内的物质代谢及其调节,科学家选择年龄、体重相同,身体健康的8名男性运动员,利用等热量的A、B两类食物做了两次实验。 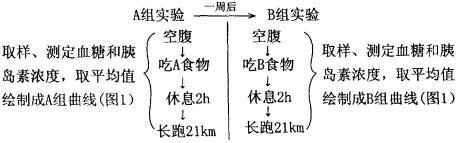
实验还测定了糖和脂肪的消耗情况(图2)。 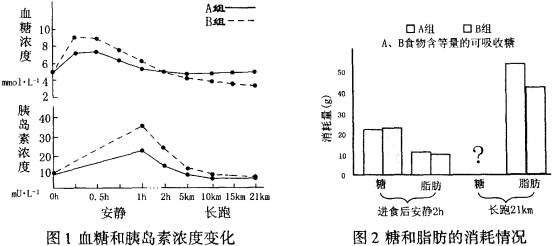
请据图分析回答问题: (1)图1显示,吃B食物后, 浓度升高,引起 浓度升高。 (2)图1显示,长跑中,A、B两组胰岛素浓度差异逐渐 ,而血糖浓度差异却逐渐 ,A组血糖浓度相对较高,分析可能是肾上腺素和 也参与了对血糖的调节,且作用相对明显,这两种激素之间具有 作用。 (3)长跑中消耗的能量主要来自糖和脂肪。研究表明肾上腺素有促进脂肪分解的作用。从能量代谢的角度分析图2,A组脂肪消耗量比B组 ,由此推测A组糖的消耗量相对 。 (4)通过检测尿中的尿素量,还可以了解运动员在长跑中 代谢的情况。 参考答案: 1.B 2.B 3.D 4.A 29.(12分) (1)生产者 第一营养级 (2)自动调节(或自净化) (3)分解作用 异养厌氧型 (4)入水口 30.(18分) (1)诱变 (2)①两(或不同) 不能 ②细胞质(或母系) (3)①高蛋白(纯合)植株 低蛋白植株(或非高蛋白植株) 后代(或F1)表现型都是高蛋白植株 ②测交方案: 用F1与低蛋白植株杂交 后代高蛋白植株和低蛋白植株的比例是1:1 或自交方案: F1自交(或杂合高蛋白植株自交) 后代高蛋白植株和低蛋白植株的比例是3:1 ③实验结果 预期结果 31.(18分) (1)血糖 胰岛素 (2)减小 增大 胰高血糖素 协同 (3)高 减少 (4)蛋白质 | 